Permutation Trees

Peter Luschny, 2010-07-20


Contents

* 1 Permutation Trees
  o 1.1 Definitions
  o 1.2 Example classifications
* 2 Permutation trees with power 4
* 3 Counting permutation trees
  o 3.1 A008292 Permutation trees of power n and width k.
  o 3.2 A179454 Permutation trees of power n and height k.
  o 3.3 A179455 Permutation trees of power n and height does not exceed k.
  o 3.4 A179456 Permutation trees of power n and height at least k.
  o 3.5 A179457 Permutation trees of power n and width does not exceed k.
* 4 The correspondence: Permutation <-> Tree
  o 4.1 Given a permutation, how to construct the associated rooted tree?
  o 4.2 Given a rooted tree, how to construct the associated permutation?
* 5 Flattening the tree: the caterpillar notation.
* 6 Summary: Three classifications of permutation trees.
* 7 The permutation trees with power 5

Definitions

A permutation tree is a labeled rooted tree that has vertex set {0,1,2,..,n} and root 0, and in which each child is larger than its parent and the children are in ascending order from the left to the right. The power of a permutation tree is the number of descendants of the root. The height of a permutation tree is the number of descendants of the root on the longest chain starting at the root and ending at a leaf. The width of a permutation tree is the number of leafs.

The correspondence with the permutation is given by traversing the periphery of the tree starting at the right hand side of the root and recording a node whenever the node's right edge is passed.

For example below the tree A has height 4 and width 1, the trees B, C, D all have height 3 and width 2, ..., and tree I has height 1 and width 4.

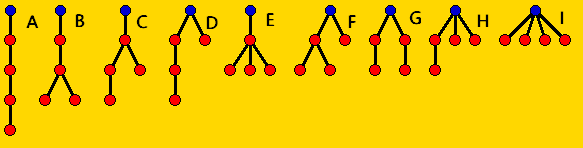
Example classifications

Permutations classified by height and by width of the associated rooted tree. Trees are coded as parental lists.

Permutations and trees, n = 3.
By width (Eulerian)
Trees Perm's #
[ 0, 1, 2] 1 2 3 1
[ 0, 1, 1]
[ 0, 1, 0]
[ 0, 0, 2]
[ 0, 0, 1]		 1 3 2
3 1 2
2 3 1
2 1 3		 4
[ 0, 0, 0] 3 2 1 1
By height
Trees Perm's #
[ 0, 0, 0] 3 2 1 1
[ 0, 0, 1]
[ 0, 0, 2]
[ 0, 1, 0]
[ 0, 1, 1]		 2 1 3
2 3 1
3 1 2
1 3 2		 4
[ 0, 1, 2] 1 2 3 1
Permutations and trees, n = 4.
By width (Eulerian)
  Trees Perm's #
A [ 0, 1, 2, 3] 1 2 3 4 1
B
C
D
G		 [ 0, 1, 2, 2]
[ 0, 1, 2, 1]
[ 0, 1, 2, 0]
[ 0, 1, 1, 3]
[ 0, 1, 1, 2]
[ 0, 1, 0, 3]
[ 0, 1, 0, 2]
[ 0, 0, 2, 3]
[ 0, 0, 2, 1]
[ 0, 0, 1, 3]
[ 0, 0, 1, 2]
 1 2 4 3
1 3 2 4
4 1 2 3
1 3 4 2
1 4 2 3
3 4 1 2
3 1 2 4
2 3 4 1
2 3 1 4
2 1 3 4
2 4 1 3		 11
E
F
H		 [ 0, 1, 1, 1]
[ 0, 1, 1, 0]
[ 0, 1, 0, 1]
[ 0, 1, 0, 0]
[ 0, 0, 2, 2]
[ 0, 0, 2, 0]
[ 0, 0, 1, 1]
[ 0, 0, 1, 0]
[ 0, 0, 0, 3]
[ 0, 0, 0, 2]
[ 0, 0, 0, 1]		 1 4 3 2
4 1 3 2
3 1 4 2
4 3 1 2
2 4 3 1
4 2 3 1
2 1 4 3
4 2 1 3
3 4 2 1
3 2 4 1
3 2 1 4		 11
I [ 0, 0, 0, 0] 4 3 2 1 1
By height
  Trees Perm's #
I [ 0, 0, 0, 0] 4 3 2 1 1
H
G
F
E		 [ 0, 0, 0, 1]
[ 0, 0, 0, 2]
[ 0, 0, 0, 3]
[ 0, 0, 1, 0]
[ 0, 0, 1, 1]
[ 0, 0, 1, 2]
[ 0, 0, 2, 0]
[ 0, 0, 2, 1]
[ 0, 0, 2, 2]
[ 0, 1, 0, 0]
[ 0, 1, 0, 1]
[ 0, 1, 0, 3]
[ 0, 1, 1, 0]
[ 0, 1, 1, 1]		 3 2 1 4
3 2 4 1
3 4 2 1
4 2 1 3
2 1 4 3
2 4 1 3
4 2 3 1
2 3 1 4
2 4 3 1
4 3 1 2
3 1 4 2
3 4 1 2
4 1 3 2
1 4 3 2		 14
D
C
B		 [ 0, 0, 1, 3]
[ 0, 0, 2, 3]
[ 0, 1, 0, 2]
[ 0, 1, 1, 2]
[ 0, 1, 1, 3]
[ 0, 1, 2, 0]
[ 0, 1, 2, 1]
[ 0, 1, 2, 2]		 2 1 3 4
2 3 4 1
3 1 2 4
1 4 2 3
1 3 4 2
4 1 2 3
1 3 2 4
1 2 4 3		 8
A [ 0, 1, 2, 3] 1 2 3 4 1

permutation trees power 4

A008292, Permutation trees of power n and width k.
(Eulerian numbers).

n\k 1 2 3 4 5 6 7 8 9
1 1
2 1 1
3 1 4 1
4 1 11 11 1
5 1 26 66 26 1
6 1 57 302 302 57 1
7 1 120 1191 2416 1191 120 1
8 1 247 4293 15619 15619 4293 247 1
9 1 502 14608 88234 156190 88234 14608 502 1

A special case: A008292(n,2) = A000295(n) for n > 1.

A179454, Permutation trees of power n and  height k.

n\k 1 2 3 4 5 6 7 8 9
1 1
2 1 1
3 1 4 1
4 1 14 8 1
5 1 51 54 13 1
6 1 202 365 132 19 1
7 1 876 2582 1289 265 26 1
8 1 4139 19404 12859 3409 473 34 1
9 1 21146 155703 134001 43540 7666 779 43 1

Special cases: A179454(n,2) = BellNumber(n) - 1 = A058692(n) for n > 1;
A179454(n,n-1) = A034856(n) for n > 1.

A179455, Permutation trees  of power n and height does not exceed k. (Partial row sums of A179454.)

n\k 1 2 3 4 5 6 7 8 9
1 1
2 1 2
3 1 5 6
4 1 15 23 24
5 1 52 106 119 120
6 1 203 568 700 719 720
7 1 877 3459 4748 5013 5039 5040
8 1 4140 23544 36403 39812 40285 40319 40320
9 1 21147 176850 310851 354391 362057 362836 362879 362880

Special cases: A179455(n, 2) = BellNumber(n) = A000110(n) for n > 1; A179455(n, n-1) = A033312(n) for n > 1.

A179456, Permutation trees of power n and  height at most n-k. (Partial row sums of A179454 starting from the diagonal.)

n\k 1 2 3 4 5 6 7 8 9
1 1
2 2 1
3 6 5 1
4 24 23 9 1
5 120 119 68 14 1
6 720 719 517 152 20 1
7 5040 5039 4163 1581 292 27 1
8 40320 40319 36180 16776 3917 508 35 1
9 362880 362879 341733 186030 52029 8489 823 44 1

A special case: A179456(n, n-1) = A000096(n).

A179457, Permutation trees of power n and width does not exceed k. (Partial row sums of A008292.)

n\k 1 2 3 4 5 6 7 8 9
1 1
2 1 2
3 1 5 6
4 1 12 23 24
5 1 27 93 119 120
6 1 58 360 662 719 720
7 1 121 1312 3728 4919 5039 5040
8 1 248 4541 20160 35779 40072 40319 40320
9 1 503 15111 103345 259535 347769 362377 362879 362880

A special case: A179457(n, 2) = A000325(n) for n > 1 (Grassmannian permutations).

Given a permutation, how to construct the associated rooted tree? Maple version.

An example use is:

tree2parent := proc(tree,n)
local j, k, parent, branch;
parent := array(1..n);
for j from 1 to nops(tree) do
  branch := tree[j];
  for k from 2 to nops(branch) do
     parent[branch[k]] := branch[k-1];
  od;
od:
convert(parent, list) end:

ListPermTrees := proc(n) local i,f,P2P;
f := combinat[permute](n);
for i from 1 to nops(f) do
  perm2tree(f[i]);
  P2P := tree2parent(%, nops(f[i])):
  lprint(f[i],"->",P2P);
od end:
 
ListPermTrees(4);

Given a rooted tree, how to construct the associated permutation?

We assume the tree given by the list of its branches, this means as the list of all the chains starting at the root of the tree and ending at a leaf.

An example use is:

RevListPermTrees := proc(n) 
local i, f, P2T, T2P;
f := combinat[permute](n);
for i from 1 to nops(f) do
  P2T := perm2tree(f[i]):
  T2P := tree2perm(P2T);
  lprint(P2T,"->",T2P);
od end:
 
RevListPermTrees(4);

Flattening the tree: the caterpillar notation

Caterpillar The image of the black-red caterpillar was made by Jill Chen from Taipei, Taiwan. It was down loaded from commons.wikimedia.org and is licensed under the Creative Commons Attribution 2.0 Generic license.

The caterpillar traverses the periphery of the tree starting at the right hand side of the root and records a node whenever he passes the node's right edge.

The caterpillar notation is the usual one line notation of a permutation augmented by the symbol '^', inserted every time when the caterpillar is forced to climb up a level in the tree. Thus it is an one dimensional description of a permutation tree. The length of the caterpillar is twice the power of the tree.

Permutations as caterpillars, n = 3
3^2^1^ 13^2^^
3^12^^
23^^1^
2^13^^		 123^^^
Permutations as caterpillars, n = 4
4^3^2^1^ 14^3^2^^
4^13^2^^
3^14^2^^
4^3^12^^
2^14^3^^
4^2^13^^
3^2^14^^
24^3^^1^
4^23^^1^
34^^2^1^
3^24^^1^
34^^12^^
23^^14^^
24^^13^^
 124^3^^^
13^24^^^
4^123^^^
14^23^^^
2^134^^^
3^124^^^
134^^2^^
234^^^1^
 1234^^^^

Segments of the caterpillar which consist entirely of numbers are called down runs and segments consisting entirely of '^'s are called up runs of the caterpillar. A run is either a up run or a down run. The number of runs and their lengths are characteristics of a permutation.

Summary: Three classifications of permutation trees.

Proposition 1. A permutation p has k down runs if and only if the permutation tree T(p) has width k.

Proposition 2. The length of the longest run of a permutation p is k if and only if the permutation tree T(p) has height k.

Proposition 1 is covered by the enumeration of permutations by the Eulerian numbers A008292 and proposition 2 by the enumeration of permutations by A179454.

The power of the caterpillar notation becomes even more obvious when we note that it immediately leads to a third classification. Just look at the tail of the caterpillar. Classifying the caterpillar by the length of the last up run gives the Stirling cycle numbers! (Definition as in CM, table 245, or DLMF, 26.13.3., ABS(A008275).) This third classification is equivalent to:

Proposition 3. Stirling cycle numbers classify permutation trees according to the length of the first (leftmost) branch.

This description is somewhat simpler then the standard definition using cycle arrangements.

The permutation trees with power 5

Permutation tree 5

Links

Rational
Trees		 Factorial
Functions		 Eulerian
Polynomials		 vonStaudt
Primes		 Irregular
Primes		 Generalized
Binomial
Bernoulli
Confusion		 Partitions
Stirling		 Zeta
Polynomials		 Perfect
Rulers		 Swinging
Primes		 Clausen
Numbers
Hadamard
Gamma		 History
Factorial		 Permutation
Trees		 Swiss
Knife		 Swinging
Factorial		 Worpitzky
Triangle