Eulerian polynomials
Peter Luschny, 2010−08−18, 2013−04−23.
The Eulerian polynomials were introduced by Leonhard Euler in his Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques in 1749 (first printed in 1765) where he describes a method of computing values of the zeta function at negative integers by a precursor of Abel's theorem applied to a divergent series. The Eulerian polynomials should not be confused with the Euler polynomials.
Definition
The Eulerian polynomials are defined by the exponential generating function
$$\sum_{n=0}^{\infty} A_{n}(t)\ \frac{x^n}{n!} = \frac{t-1}{t-\exp((t-1)x)}.$$The Eulerian polynomials can be computed by recurrence:
$$A_{0}(t) = 1, $$ $$A_{n}(t) = t(1-t)A'_{n-1}(t)+A_{n-1}(t)(1+(n-1)t) \quad (n \ge 1)\,. $$An equivalent way to write this definition is to set the Eulerian polynomials inductively by
$$A_{0}(t) = 1,$$ $$A_{n}(t) = \sum_{k=0}^{n-1} {n \choose k} A_{k}(t)(t-1)^{n-1-k} \quad (n \ge 1)\,.$$The definition given is used by major authors like D. E. Knuth, D. Foata and F. Hirzebruch. In the older literature (for example in L. Comtet, Advanced Combinatorics) a slightly different definition is used, namely
$$C_{0}(t) = 1,\, $$ $$C_{n}(t) = t(1-t)C'_{n-1}(t) + C_{n-1}(t)(nt) \quad (n \ge 1)\,. $$The sequence of Eulerian polynomials $A_n(x)$ has ordinary generating function given by the continued fraction
$$\cfrac{1}{1 - t + \cfrac{x\, t^2}{(2+x)\, t - 1 + \cfrac{4x\, t^2}{(3+2x)\, t - 1 + \cfrac{9x\, t^2}{(4+3x)\, t - 1 + \cfrac{16x\, t^2}{\cdots}}}}} $$Three identities
An identity due to Euler is
$$ \sum_{j \ge 0} x^j(j+1)^n = \frac{A_n(x)}{(1-x)^{n+1}}. $$For instance we get for $ n\,=\,0,1,2: $
$$ 1 + x + x^2 + x^3 + ... = \frac{1}{1-x}, $$ $$ 1 + 2x + 3x^2 + 4x^3 + ... = \frac{1}{(1-x)^2}, $$ $$ 1 + 2^2 x + 3^2 x^2 + 4^2 x^3 + ... = \frac{1+x}{(1-x)^3}. $$Let $\operatorname{S}(n,k)$ denote the Stirling numbers of the second kind. Frobenius proved that the Eulerian polynomials are equal to:
$$ A_n(x) = \sum_{k=1}^{n} k! \, \operatorname{S}(n,k)(x-1)^{n-k} \quad (n \ge 1). $$The third identity is called Worpitzky's identity
$$ x^n = \sum_{0 \le k \le n } \binom{x+k}{n} [x^k] A_n(x). $$Here $ [x^k] A_n(x) $ denotes the coefficient of $ x^k $ in $ A_n(x) $.
Eulerian numbers
The coefficients of the Eulerian polynomials are the Eulerian numbers $A_{n,k}$ [1],
$$A_{n}(t) = \sum_{k=0}^{n} A_{n,k}\ t^{k}.$$This definition of the Eulerian numbers agrees with the combinatorial definition in the DLMF[2]. The triangle of Eulerian numbers is also called Euler's triangle [3].
|
|
|
Euler's definition $A_{n,k}$ is A173018. The main entry for the Eulerian numbers in the OEIS database is A008292. It enumerates like $C_{n,k}$ albeit restricted to n ≥ 1 and k ≥ 1.
The combinatorial interpretation
Let $S_n$ denote the set of all bijections (one-to-one and onto functions) from $\{1, 2, \ldots, n \}$ to itself, call an element of $S_n$ a permutation p and identify it with the ordered list $p_1p_2\ldots p_n $ .
Using the Iverson bracket [.] the number of ascents of p is defined as
$$\operatorname{asc}(p) = \sum_{i=1}^n \left[\, p_{i} \lt p_{i+1} \, \right], $$where pn+1 ← 0. The combinatorial interpretation of the Eulerian polynomials is then given by
$$A_{n}(x) = \sum_{p \in S_n} x^{\operatorname{asc}(p)} .$$The table below illustrates this representation for the case $n = 4. $
| p | asc | p | asc | p | asc | p | asc |
| 4321 | 0 | 4231 | 1 | 2413 | 2 | 1423 | 2 |
| 3214 | 1 | 2431 | 1 | 2134 | 2 | 1342 | 2 |
| 3241 | 1 | 4312 | 1 | 2314 | 2 | 4123 | 2 |
| 3421 | 1 | 3142 | 1 | 2341 | 2 | 1324 | 2 |
| 4213 | 1 | 4132 | 1 | 3124 | 2 | 1243 | 2 |
| 2143 | 1 | 1432 | 1 | 3412 | 2 | 1234 | 3 |
History

|
Leonhard Euler introduced the polynomials in 1749 [4] in the form
$$\sum_{k=0}^{\infty} (k+1)^{n}\ t^{k} = \frac{A_{n}(t)}{(1-t)^{n+1}}.$$Euler introduced the Eulerian polynomials in an attempt to evaluate the Dirichlet eta function
$$\eta(s) = \sum_{n=1}^{\infty}{\frac{(-1)^{n-1}}{n^s}}$$at $s = -1, -2, -3,\ldots $. This led him to conjecture the functional equation of the eta function (which immediately implies the functional equation of the zeta function). Most simply put, the relation Euler was after was
$$\zeta(-n) = \frac{A_{n}(-1)}{2^{n+1}-4^{n+1}} \quad (n \ge 0)\ .$$Though Euler's reasoning was not rigorous by modern standards it was a milestone on the way to Riemann's proof of the functional equation of the zeta function. A short exposition of what Euler did was given by Keith Conrad on MathOverflow.
The facsimile shows Eulerian polynomials as given by Euler in his work Institutiones calculi differentialis, 1755. It is interesting to note that the original definition of Euler coincides with the definition in the DLMF, 2010.
Eulerian generating functions
We call a generating function an Eulerian generating function iff it has the form
$$G_{n}(t) = \frac{g(t) A_{n}(t)}{(1-t)^{n+1}}, \quad (n \ge 0)$$for some polynomial g(t). Many elementary classes of sequences have an Eulerian generating function. A few examples are collocated in the table below.
| n = 0 | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | |
| g(t) = 1 − t2 | A019590 | A040000 | A008574 | A005897 | A008511 | A008512 |
| g(t) = 1 − t | A000007 | A000012 | A005408 | A003215 | A005917 | A022521 |
| g(t) = t | A057427 | A001477 | A000290 | A000578 | A000583 | A000584 |
| g(t) = 1 + t | A040000 | A005408 | A001844 | A005898 | A008514 | A008515 |
| g(t)=1+t+t2 | A158799 | A008486 | A005918 | A027602 | A160827 | A179995 |
For instance the case
- g(t) = t gives the generating function of the regular orthotopic numbers,
- g(t) = 1 + t gives the generating function of the centered orthotopic numbers.
The roots of the polynomials

|
A1(x) , A2(x) , A3(x) , A4(x) , A5(x) , A6(x) |
$ A_n(x) $ has only (negative and simple) real roots, a result due to Frobenius. In fact the Eulerian polynomials form a Sturm sequence, that is, $ A_{n+1}(x) $ has n real roots separated by the roots of $ A_{n}(x) $.
Special values
| x | −1/2 | 1/2 | 3/2 |
| 2nAn(x) | A179929 | A000629 | A004123 |
| x | −2 | −1 | 0 |
| An(x) | A087674 | A155585 | A000012 |
| x | 1 | 2 | 3 |
| An(x) | A000142 | A000670 | A122704 |
Assorted sequences and formulas
Let ∂r denote the denominator of a rational number r.
| A122778 | An(n) |
| A180085 | An(−n) |
| A000111 | An(I)(1+I)(1-n) |
| A006519 | ∂(An(−1) / 2n) |
| A001511 | log2(∂(A2n+1(−1) / 22n+1)) |
Eulerian polynomials $A_{n}(x)$ and Euler polynomials $E_{n}(x)$ have a sequence of values in common (up to a binary shift). Let $B_{n}(x)$ denote the Bernoulli polynomials and ζ(n) the Riemann Zeta function. $\left\{{n \atop k}\right\}\,$ denotes the Stirling numbers of the second kind. The formulas below show how rich in content the Eulerian polynomials are.
|
A155585 for all $n \ge 0$ |
| $\quad A_{n}(-1) $ |
| $= E_{n}(1) 2^n $ |
| $= \zeta(-n)(2^{n+1}-4^{n+1}) $ |
| $= B_{n+1}(1) \frac{4^{n+1}-2^{n+1}}{n+1} $ |
| $= \sum_{k=0}^n \left\{ {n\atop k} \right\} (-2)^{n-k} k! $ |
| $= \sum_{k=0}^n \sum_{v=0}^k {k \choose v} (-1)^v 2^{n-k}(v+1)^n $ |
The connection with the polylogarithm
Eulerian polynomials are related to the polylogarithm
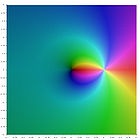
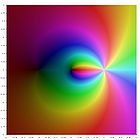
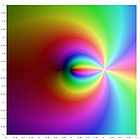
$$ \operatorname{Li}_s(z) = \sum_{k=1}^\infty {z^k \over k^s}.$$For nonpositive integer values of s, the polylogarithm is a rational function. The first few are
| $ \operatorname{Li}_{0}(z) = {z \over 1-z}; $ | $ \operatorname{Li}_{-1}(z) = {z \over (1-z)^2}; $ |
| $ \operatorname{Li}_{-2}(z) = {z(1+z) \over (1-z)^3}; $ | $ \operatorname{Li}_{-3}(z) = {z(1+4z+z^2) \over (1-z)^4} . $ |
A plot of these functions in the complex plane is given in the gallery [6] below.
| $\operatorname{Li}_{0}(z) $ | $\operatorname{Li}_{-1}(z)$ | $\operatorname{Li}_{-2}(z)$ | $\operatorname{Li}_{-3}(z)$ |
In general the explicit formula for nonpositive integer s is
$$\operatorname{Li}_{-n}(z) = {{z A_n(z)} \over (1-z)^{n+1}} \qquad (n \ge 0) ~.$$See also DLMF and the section on series representations of the polylogarithm on Wikipedia. However, note that the conventions on Wikipedia do not conform to the DLMF definition of the Eulerian polynomials.
The connection with cardinal B-splines
The cardinal B-spline of the first order $b_1(n)$ is the characteristic function of the unit interval. The cardinal B-spline of order $n>1$ is $b_n(x) = \int_{0}^{1} b_{n-1}(x-t) \, dt$. Then for $n \gt 0$
$$ A_n(x) = n! \, \sum_{k=0}^{n-1} b_{n+1}(k+1)x^k . $$This representation of the Eulerian polynomials suggests to look also at the midpoint Eulerian polynomials
$$ M_n(x) = 2^{n} n! \, \sum_{k=0}^{n} b_{n+1}(k+1/2)x^k . $$The midpoint Eulerian polynomials
Generating function
The midpoint Eulerian polynomials are defined by the generating function
$$ \sum_{n=0}^{\infty} \frac{M_{n}(t)}{(t-1)^n} \, \frac{x^n}{2^n n!} = \frac{t-1}{t-e^x} e^{x/2},$$which is the counterpart to the generating function of the standard Eulerian polynomials
$$ \sum_{n=0}^{\infty} \frac{A_{n}(t)}{(t-1)^n} \, \frac{x^n}{n!} = \frac{t-1}{t-e^x}. $$Exponential generating function
$$\sum_{n=0}^{\infty} M_{n}(x)\ \frac{t^n}{n!} = \frac{(1-x)\exp((1-x)t)}{1-x\exp(2(1-x)t)}.$$Recurrence relation
The midpoint Eulerian polynomials can be computed by recurrence:
$$M_{0}(t) = 1, $$ $$M_{n}(t) = 2t(1-t)M'_{n-1}(t)+M_{n-1}(t)(1+(2n-1)t) \quad (n \ge 1)\,. $$Expansion
The expansion analogous to Euler's given above is
$$ \sum_{j \ge 0} x^j(2j+1)^n = \frac{M_n(x)}{(1-x)^{n+1}}. $$For instance we get for $ n\,=\,0,1,2: $
$$ 1 + x + x^2 + x^3 + ... = \frac{1}{1-x}, $$ $$ 1 + 3x + 5x^2 + 7x^3 + ... = \frac{1+x}{(1-x)^2}, $$ $$ 1 + 3^2 x + 5^2 x^2 + 7^2 x^3 + ... = \frac{1+6x+x^2}{(1-x)^3}. $$Worpitzky-type identity
$$ (2x+1)^{n} = \sum_{0 \le k \le n } \binom{x+k}{n} [x^k] M_n(x). $$Roots of the polynomials
$M_n(x)$ has $n$ zeros which are simple and negative.
The midpoint Eulerian numbers
The coefficients of the midpoint Eulerian polynomials are the midpoint Eulerian numbers $M_{n,k}$
$$M_{n}(t) = \sum_{k=0}^{n} M_{n,k}\ t^{k}.$$| Mn,k | 0 | 1 | 2 | 3 | 4 | row sum |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 2 |
| 2 | 1 | 6 | 1 | 0 | 0 | 8 |
| 3 | 1 | 23 | 23 | 1 | 0 | 48 |
| 4 | 1 | 76 | 230 | 76 | 1 | 384 |
Note that the offset in our setup is $(n,k) = (0,0)$ which differs from the offset assumed in some of the formulas in A060187.
The combinatorial interpretation
Let $B_n$ denote the set of signed permutations of $$ I = \{ \pm i \ : \ 1 \le i \le n \} $$ such that $p(-i) = -p(i)$ for all $i \in I$. The descent number of $p$ is defined as $$ des(p) = \operatorname{card} \{i \in [n]: p(i-1) \gt p(i)\} $$ where $p(0) = 0$. Then $$ M_n(x) = \sum_{p \in B_n} x^{des(p)}.$$
The table below illustrates this representation for the case $n = 2.$
| p | des | p | des |
| -2, -1, 1, 2 | 0 | 1, -2, 2, -1 | 1 |
| -2, 1, -1, 2 | 1 | 1, 2, -2, -1 | 1 |
| -1, -2, 2, 1 | 1 | 2, -1, 1, -2 | 1 |
| -1, 2, -2, 1 | 1 | 2, 1, -1, -2 | 2 |
The connection with the Lerch transcendent
Since the Lerch transcendent $\Phi(z,s,a) = \sum_{k=0}^{\infty} \frac{z^k}{(a+k)^s}$ (the analytic continuation is always implied) is related to the polylogarithm by $ \operatorname{Li}_s(z) = z\Phi(z,s,a)$ the formula given above shows
$$ \Phi(z,-n,1) = { {A_n(z)} \over (1-z)^{n+1}} \qquad (n \ge 0) ~.$$Similarly one finds for the midpoint Eulerian polynomials
$$ 2^n \Phi(z,-n,1/2) = { {M_n(z)} \over (1-z)^{n+1}} \qquad (n \ge 0) ~.$$The Eulerian polynomials generalized
The formulas in the last section suggest to introduce the following generalization of the Eulerian polynomials $A_{n,k}(z)$.
$$ k^n \Phi(z,-n,1/k) = { {A_{n,k}(z)} \over (1-z)^{n+1}} \qquad (n \ge 0, k \ge 1, z \ne 1) \qquad \text{(*)}$$Thus $A_{n,1}(z)=A_{n}(z)$ and $A_{n,2}(z)=M_{n}(z)$.
|
|
Plugging $z=1$ into the left hand side of (*) times $ (1-z)^{n+1} $ would set $A_{n,k}(1)=0$. On the other hand the row sums of the coefficients of $A_{n,k}(z)$ are $k^n n! $ (the k-factorial numbers, A000142, A000165, A032031,…). But taking the limit will reconcile the two values $$A_{n,k}(1) = \lim_{z \rightarrow 1} \ k^n (1-z)^{n+1} \Phi(z,-n,1/k) = k^n n! .$$
The most interesting point to evaluate these polynomials at is $z=-1$ (this is what Euler did in the classical case).
| $A_{n,1}(-1)$ | A155585 | 1, 1, 0, -2, 0, 16, 0, -272, 0, 7936, 0, |
| $A_{n,2}(-1)$ | A002436 | 1, 0, -4, 0, 80, 0, -3904, 0, 354560, 0, |
| $A_{n,3}(-1)$ | A000810 | 1, -1, -8, 26, 352, -1936, -38528, 297296, |
| $A_{n,4}(-1)$ | A079858 | 1, -2, -12, 88, 912, -11552, -176832, |
(Note that in OEIS sequences are written zero-suppressed if every other term is $0$ and that we refer to a sequence in the database even if it has a different sign pattern.)
If $0 \le n$ is integer and $0 \lt a$ is real then [5] $$ \Phi(z,-n,a) = a^n + \sum_{j=0}^{n} \binom{n}{j} \operatorname{Li}_{-j}(z) a^{n-j}. $$
Thus with $k = 1/a$ for some integer $k \gt 0$ the generalized Eulerian polynomials can be written $$ A_{n,k}(z) = \left(1-z \right)^{n+1} \left(1 + \sum_{j=0}^{n} \binom{n}{j} \operatorname{Li}_{-j}(z) k^{j} \right) \qquad (z \ne 1) . $$
Here the index $k$ is used for integer values of $k$ but it can also be seen as an arbitrary positive real. For example we get
| $2^n A_{n,1/2}(-1)$ | A119881 | 1, 3, 8, 18, 32, 48, 128, 528, 512, |
| $3^n A_{n,1/3}(-1)$ | A225116 | 1, 5, 24, 110, 480, 2000, 8064, 32240, |
| $ 2^n A_{n,1/2}(2) $ | A052841 | 1, 0, 2, 6, 38, 270, 2342, 23646, |
Assorted values of the polynomials
| A(n, k, I) * (1+I)^(1-n) |
k = 1 | k = 2 | k = 3 | k = 4 |
| Re | A000111 | A001586 | A007286 | A006873 |
| Im | A000007 | A001586 | A007289 | A225109 |
| A(n, k, I) * (1-I)^(1-n) |
k = 1 | k = 2 | k = 3 | k = 4 |
| Re | A155585 | A188458 | A000810 | A000813
A156205 |
| Im | A122045 | A212435 | A225147 | A156201 |
Among other numbers we see the Euler (or up/down) numbers, the generalized Euler numbers (Springer numbers), the number of alternating k-signed permutations and two recent additions triggered by this exploration. (As always the references are modulo sign and suppressed zeros.)
How to compute Eulerian polynomials.
The definitions given above are not computer friendly. Maple for example makes errors when computing the Lerch transcendent (as far as I know in all versions throughout the years 1998--2012) and gives wrong values if formula (*) is used. A computation based on the polylogarithm is much better, still the polylogarithm is not a trivial function to implement.
To the rescue come the cardinal splines (see the Schoenberg reference; Schoenberg elucidates the cases $ k=1 $ and $ k=2 $ in detail).
Cardinal B-splines are easy to compute and the Eulerian polynomials can be based on them. Despite their modern name B-splines were first investigated by Nikolai Lobachevsky in the nineteenth century.

@CachedFunction
def B(n, x): # Cardinal B-splines
if n == 1: return 0 if (x < 0) or (x >= 1) else 1
return (x/(n-1))*B(n-1, x)+((n-x)/(n-1))*B(n-1, x-1)
def EulerianPolynomial(n, k, x):
if n == 0: return 1
return k^n*factorial(n)*add(B(n+1, m+1/k)*x^m for m in (0..n))
For example:
[EulerianPolynomial(n, 4, x) for n in (0..5)] [imag(-(1-I)^(1-n)*EulerianPolynomial(n,4,I)) for n in (0..17)] # A156201
No library functions besides the power and factorial function are used. And the factor $ k^n n! $ can be integrated into the recurrence.
@CachedFunction
def EB(n, k, x):
if n == 1: return 0 if (x < 0) or (x >= 1) else 1
return k*x*EB(n-1, k, x) + k*(n-x)*EB(n-1, k, x-1)
def EulerianPolynomial(n, k, x):
if n == 0: return 1
return add(EB(n+1, k, m+1/k)*x^m for m in (0..n))
Also the rational parameter $ m+1/k $ can be eliminated.
@CachedFunction
def BB(n, k, x):
if n == 1: return 0 if (x < 0) or (x >= k) else 1
return x*BB(n-1, k, x) + (n*k-x)*BB(n-1, k, x-k)
def EulerianPolynomial(n, k, x):
if n == 0: return 1
return add(BB(n+1, k, k*m+1)*x^m for m in (0..n))
Based on this recurrence a closed form can also be given if we use the signum function defined $ \operatorname{sgn}(x-y) = -1 \text{ if } x \lt y; 0 \text{ if } x = y; 1 \text{ if } x \gt y.\ $ Then
def EulerianPolynomial(n, k, x) :
if n == 0: return 1
S = lambda m: add((-1)^j*binomial(n+1,j)*(k*(m-j)+1)^n*sgn(k*(m-j)+1)
for j in (0..n+1))
return add(S(m)*x^m for m in (0..n))/2
Finally calling the coefficients of the (generalized) Eulerian polynomials (generalized) Eulerian numbers we arrive at the recurrence:
@CachedFunction
def EulerianNumber(n, k, m) :
if n == 0: return 1 if m == 0 else 0
return (k*(n-m+1)-1)*EulerianNumber(n-1,k,m-1)
+ (m*k+1)*EulerianNumber(n-1,k,m)
def EulerianPolynomial(n, k, x):
return add(EulerianNumber(n, k, m)*x^m for m in (0..n))
The generalized Eulerian polynomials can also be computed by a function recurrence: $$A_{0,k}(t) = 1, $$ $$A_{n,k}(t) = kt(1-t)A'_{n-1,k}(t)+A_{n-1,k}(t)(1+(kn-1)t) \quad (n \ge 1)\,. $$
Generating function
A generating function for the generalized Eulerian polynomials $ A_{n,k}(x) $ is
$$ \operatorname{GF}(n; k) = k^n n! \, \left( 1 /x - 1 \right) ^{n+1} \, [t^n] \, x e^{\frac {tx}{k} } \left( 1-x e^{tx} \right) ^{-1}. $$Here $ [t^n]f(t,x) $ is the coefficient of $ t^n$ in $ f(t,x) $.
This generating function immediately suggests a more symmetric generalization with two parameters:
$$ \operatorname{GF}(n; k, m) = (km)^n n! \, \left( 1 /x - 1 \right) ^{n+1} \, [t^n] \, x e^{\frac {tx}{k} } \left( 1-x e^{\frac {tx}{m}} \right) ^{-1}. $$Summary
$$ \sum_{j \ge 0} z^j(kj+1)^n = k^n \Phi(z,-n,1/k) = { {A_{n,k}(z)} \over (1-z)^{n+1}} = 1 + \sum_{j=0}^{n} \binom{n}{j} \operatorname{Li}_{-j}(z) k^{j} $$ $$ \begin{align*} a_{0, k}( m)& = [ k=0 ] \\ a_{n, k}( m)& = (m(n-k+1)-1)a_{n-1, k-1}(m) + (mk+1)a_{n-1, k}(m) \end{align*} $$ $$ A_{n,k}(z) = \sum_{m=0}^n a_{n, m}(k)z^m $$Short table $A_{n,k}(x)$
$$A_{0,k}(x) = 1$$ $$A_{1,k}(x) = (k - 1)\,x + 1$$ $$A_{2,k}(x) = (k^{2} - 2\,k + 1)\,x^{2} + (k^{2} + 2\,k - 2)\,x + 1$$ $$A_{3,k}(x) = (k^{3} - 3\,k^{2} + 3\,k - 1)\,x^{3} + (4\,k^{3} - 6\,k + 3)\,x^{2} + (k^{3} + 3\,k^{2} + 3\,k - 3)\,x + 1$$ $$ A_{4,k}(x) = (k^{4} - 4\,k^{3} + 6\,k^{2} - 4\,k + 1)\,x^{4} + (11\,k^{4} - 12\,k^{3} - 6\,k^{2} + 12\,k - 4)\,x^{3} + \ldots $$ $$ \qquad\qquad \ldots \ (11\,k^{4} + 12\,k^{3} - 6\,k^{2} - 12\,k + 6)\,x^{2} + (k^{4} + 4\,k^{3} + 6\,k^{2} + 4\,k - 4)\,x + 1 $$
Program
(Maple)
a := proc(n, m) local k; # Eulerian numbers
add((-1)^k*binomial(n+1, k)*(m+1-k)^n, k=0..m)
end:
A := proc(n, x) local k; # Eulerian polynomials
add(a(n, k)*x^k, k=0..n)
end:
ma := proc (n, m) local k; # Midpoint Eulerian numbers
add((-1)^(m-k)*binomial(n+1, m-k)*(2*k+1)^n, k=0..m)
end:
mr := proc(n, k) option remember; # Recursive mid. Eul.num.
if n = 0 then if k=0 then 1 else 0 fi else
(2*(n-k)+1)*mr(n-1, k-1) + (2*k+1)*mr(n-1, k) fi
end:
MA := proc(n, x) local k; # Midpoint Eulerian polynomials
add(mr(n, k)*x^k, k=0..n)
end:
B := proc(n, u) option remember; # Cardinal B-splines
if n = 1 then if (u < 0) or (u >= 1) then 0 else 1 fi
else (u/(n-1))*B(n-1, u)+((n-u)/(n-1))*B(n-1, u-1) fi
end:
# Generalized Eulerian polynomials based on polylog.
EulerianPolynomial := proc(n, k, x) local j;
if x = 1 then k^n*n! else
(1-x)^(1+n)*(1+add(binomial(n,j)*polylog(-j,x)*k^j,j=0..n));
simplify(expand(%)) fi
end:
# Generalized Eulerian polynomials based on direct recurrence.
EulerianPolynomials := proc(n, k, t)
if n = 0 then 1 else
k*t*(1-t)*diff(EulerianPolynomials(n-1,k,t),t)
+EulerianPolynomials(n-1,k,t)*(1+(k*n-1)*t) fi;
sort(simplify(expand(%))) end:
# Generating function, general case
gf := proc(n, k) local f;
f := (x,t) -> x*exp(t*x/k)/(1-x*exp(t*x));
series(f(x,t), t, n+2); ((1-x)/x)^(n+1)*k^n*n!*coeff(%, t, n);
collect(simplify(%), x) end:
seq(print(gf(n, k)), n=0..4); # generates the table above
(Sage)
def a(n, m) : # Eulerian numbers
return add((-1)^k*binomial(n+1, k)*(m+1-k)^n for k in (0..m))
def A(n, x) : # Eulerian polynomials
return add(a(n, k)*x^k for k in (0..n))
def ma(n, m): # Midpoint Eulerian numbers
return add((-1)^(m-k)*binomial(n+1, m-k)*(2*k+1)^n for k in (0..m))
@CachedFunction
def mr(n, k) : # Recursive midpoint Eulerian numbers
if n == 0: return 1 if k == 0 else 0
return (2*(n-k)+1)*mr(n-1, k-1) + (2*k+1)*mr(n-1, k)
def MA(n, x): # Midpoint Eulerian polynomials
return add(mr(n, k)*x^k for k in (0..n))
@CachedFunction
def B(n, x): # Cardinal B-splines
if n == 1: return 0 if (x < 0) or (x >= 1) else 1
return (x/(n-1))*B(n-1, x)+((n-x)/(n-1))*B(n-1, x-1)
@CachedFunction
def BB(n, k, x): # Modified Cardinal B-splines
if n == 1: return 0 if (x < 0) or (x >= k) else 1
return x*BB(n-1, k, x) + (n*k-x)*BB(n-1, k, x-k)
# Generalized Eulerian polynomials based on recurrence.
def EulerianPolynomial(n, k, x):
if n == 0: return 1
return add(BB(n+1, k, k*m+1)*x^m for m in (0..n))
# Generalized Eulerian polynomials based on direct recurrence.
def EulerianPolynomials(n, k, t):
if n == 0 : return 1
return (k*t*(1-t)*diff(EulerianPolynomials(n-1,k,t),t)
+ EulerianPolynomials(n-1,k,t)*(1+(k*n-1)*t)).expand()
# Generalized Eulerian polynomials based on polylog.
from mpmath import *
mp.dps = 32; mp.pretty = True
def EulerianPolynomialLi(n, k, x):
if x == 1: return k^n*factorial(n)
return (1-x)^(1+n)*(1+add(binomial(n,j)*polylog(-j,x)*k^j
for j in (0..n)))
Notes
- ↑ The Eulerian number $A_{n,k}$ is not to be confused with the value of the nth Eulerian polynomial at k. For instance $A_{n,n} = 1,0,0,0,\ldots$ whereas $A_{n}(n)$ is A122778.
- ↑ Digital Library of Mathematical Functions, National Institute of Standards and Technology, Table 26.14.1
- ↑ The name Euler's triangle is used, for example, in Concrete Mathematics, Table 254. A virtue of this name is that it might evoke an association to Pascal's triangle, with which it shares the symmetry between left and right.
- ↑ Euler read his paper in the Königlichen Akademie der Wissenschaften zu Berlin in the year 1749 ("Lu en 1749"). It was published only much later in 1768.
- ↑ See the formula at Wolfram research.
- ↑ Author of the plots of the polylogarithm functions in the complex plane: Jan Homann. Public domain.
References
- P. Barry, Eulerian Polynomials as Moments, via Exponential Riordan Arrays, Journal of Integer Sequences, Vol. 14 (2011), Article 11.9.5.
- K. Conrad, Answer to: Historical question in analytic number theory, MathOverflow, Jan 29 2010.
- Leonhard Euler, Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques, 1768. E352 (Eneström Index), The Euler Archive.
- Leonhard Euler, Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum, 1755. E212 (Eneström Index), The Euler Archive.
- Dominique Foata, Eulerian Polynomials: from Euler's Time to the Present. February 18, 2008.
- Dominique Foata and Marcel-Paul Schützenberger, Théorie Géométrique des Polynômes Eulériens, 1970.
- G. Frobenius, Über die Bernoullischen Zahlen und die Eulerschen Polynome. Sitzungsberichte der Preussischen Akad. der Wiss., Phys.-Math. Kl. (1910), 809–847.
- R. L. Graham, D. E. Knuth and O. Patashnik, Concrete Mathematics, 1989.
- Friedrich Hirzebruch, Eulerian polynomials, Münster J. of Math. 1 (2008), 9–14.
- W. Quade and L. Collatz, Zur Interpolationstheorie der reellen periodischen Funktionen. Sitzungsbericht der Preuss. Akad. der Wiss., Phys.-Math. Kl., (1938), 383–429.
- I. J. Schoenberg, Cardinal interpolation and spline functions IV. The exponential Euler splines. ISNM 20 (1972), 382–404.
The first part of this article was originally written for the OeisWiki. Thanks to Daniel Forgues for editorial help.