Eulerian polynomials

Definition

The Eulerian polynomials are defined by the exponential generating function

\sum_{n = 0}^{\infty} A_{n} (t) \frac{x^{n}}{n!} = \frac{t - 1}{t - exp ((t - 1) x)} .

The Eulerian polynomials can be computed by recurrence:

A_{0} (t) = 1,

A_{n} (t) = t (1 - t) A_{n - 1}^{'} (t) + A_{n - 1} (t) (1 + (n - 1) t) (n \geq 1) .

An equivalent way to write this definition is to set the Eulerian polynomials inductively by

A_{0} (t) = 1,

A_{n} (t) = \sum_{k = 0}^{n - 1} (\binom{n}{k}) A_{k} (t) (t - 1)^{n - 1 - k} (n \geq 1) .

The definition given is used by major authors like D. E. Knuth, D. Foata and F. Hirzebruch. In the older literature (for example in L. Comtet, Advanced Combinatorics) a slightly different definition is used, namely

C_{0} (t) = 1,

C_{n} (t) = t (1 - t) C_{n - 1}^{'} (t) + C_{n - 1} (t) (n t) (n \geq 1) .

Eulerian numbers

The coefficients of the Eulerian polynomials are the Eulerian numbers $A_{n, k}$ ^[1],

A_{n} (t) = \sum_{k = 0}^{n - 1} A_{n, k} t^{k} .

This definition of the Eulerian numbers agrees with the combinatorial definition in the DLMF^[2]. The triangle of Eulerian numbers is also called Euler's triangle^[3].

A_n,k	0	1	2	3	4
0	1	0	0	0	0
1	1	0	0	0	0
2	1	1	0	0	0
3	1	4	1	0	0
4	1	11	11	1	0

C_n,k	0	1	2	3	4
0	1	0	0	0	0
1	0	1	0	0	0
2	0	1	1	0	0
3	0	1	4	1	0
4	0	1	11	11	1

Euler's definition $A_{n, k}$ is A173018. The main entry for the Eulerian numbers in the database is A008292. It enumerates $C_{n, k}$ with offset (1,1).

The combinatorial interpretation

Let $S_{n}$ denote the set of all bijections (one-to-one and onto functions) from ${1, 2, \dots, n}$ to itself, call an element of $S_{n}$ a permutation p and identify it with the ordered list $p_{1} p_{2} \dots p_{n}$ .

Using the Iverson bracket [.] the number of ascents of p is defined as

asc (p) = \sum_{i = 1}^{n} [p_{i} < p_{i + 1}],

where $p_{n + 1} \leftarrow 0$ . The combinatorial interpretation of the Eulerian polynomials is then given by

A_{n} (x) = \sum_{p \in S_{n}} x^{asc (p)} .

The table below illustrates this representation for the case n = 4.

p	asc	p	asc	p	asc	p	asc
4321	0	4231	1	2413	2	1423	2
3214	1	2431	1	2134	2	1342	2
3241	1	4312	1	2314	2	4123	2
3421	1	3142	1	2341	2	1324	2
4213	1	4132	1	3124	2	1243	2
2143	1	1432	1	3412	2	1234	3

The number of permutations of {1, 2, …, n} with n ascents (the central Eulerian numbers) are listed in A180056.

History

Eulerian Polynomials, Institutiones calculi differentialis, 1755

Eulerian polynomials in Institutiones calculi differentialis, 1755

Leonhard Euler introduced the polynomials in 1749 ^[4] in the form

\sum_{k = 0}^{\infty} (k + 1)^{n} t^{k} = \frac{A_{n} (t)}{(1 - t)^{n + 1}} .

Euler introduced the Eulerian polynomials in an attempt to evaluate the Dirichlet eta function

η (s) = \sum_{n = 1}^{\infty} \frac{(- 1)^{n - 1}}{n^{s}}

at $s = - 1, - 2, - 3, \dots$ . This led him to conjecture the functional equation of the eta function (which immediately implies the functional equation of the zeta function). Most simply put, the relation Euler was after was

A_{n} (- 1) = (2^{n + 1} - 4^{n + 1}) ζ (- n) (n \geq 0) .

Though Euler's reasoning was not rigorous by modern standards it was a milestone on the way to Riemann's proof of the functional equation of the zeta function.

The facsimile shows Eulerian polynomials as given by Euler in his work Institutiones calculi differentialis, 1755. It is interesting to note that the original definition of Euler coincides with the definition in the DLMF, 2010.

Eulerian generating functions

We call a generating function an Eulerian generating function iff it has the form

G_{n} (t) = \frac{g (t) A_{n} (t)}{(1 - t)^{n + 1}}, (n \geq 0)

for some polynomial g(t). Many elementary classes of sequences have an Eulerian generating function. A few examples are collocated in the table below.

Generating function $\frac{g (t) A_{n} (t)}{(1 - t)^{n + 1}}$	n = 0	n = 1	n = 2	n = 3	n = 4	n = 5
g(t) = 1 − t²	A019590	A040000	A008574	A005897	A008511	A008512
g(t) = 1 − t	A000007	A000012	A005408	A003215	A005917	A022521
g(t) = t	A057427	A001477	A000290	A000578	A000583	A000584
g(t) = 1 + t	A040000	A005408	A001844	A005898	A008514	A008515
g(t) = 1 + t + t²	A158799	A008486	A005918	A027602	A160827	A179995

For instance the case

$g (t) = t$ gives the generating function of the regular orthotopic numbers,
$g (t) = 1 + t$ gives the generating function of the centered orthotopic numbers.

Plot

A₁(x) , A₂(x) , A₃(x) , A₄(x) , A₅(x) , A₆(x)

Special values of the Eulerian polynomials

x	−1/2	1/2	3/2
2ⁿA_n(x)	A179929	A000629	A004123
x	−2	−1	0
A_n(x)	A087674	A155585	A000012
x	1	2	3
A_n(x)	A000142	A000670	A122704

Assorted sequences and formulas

Let ∂r denote the denominator of a rational number r.

A122778	A_n(n)
A180085	A_n(−n)
A006519	∂(A_n(−1) / 2ⁿ)
A001511	log₂(∂(A_2n+1(−1) / 2²ⁿ⁺¹))

Eulerian polynomials $A_{n} (x)$ and Euler polynomials $E_{n} (x)$ have a sequence of values in common (up to a binary shift). Let $B_{n} (x)$ denote the Bernoulli polynomials and ζ(n) the Riemann Zeta function. $\{\binom{n}{k}\}$ denotes the Stirling numbers of the second kind. The formulas below show how rich in content the Eulerian polynomials are.

A155585 for all n ≥ 0
	$A_{n} (- 1)$
	$= E_{n} (1) 2^{n}$
	$= ζ (- n) (2^{n + 1} - 4^{n + 1})$
	$= B_{n + 1} (1) \frac{4^{n + 1} - 2^{n + 1}}{n + 1}$
	$= \sum_{k = 0}^{n} \{\binom{n}{k}\} (- 2)^{n - k} k!$
	$= \sum_{k = 0}^{n} \sum_{v = 0}^{k} (\binom{k}{v}) (- 1)^{v} 2^{n - k} (v + 1)^{n}$

The connection with the polylogarithm

Eulerian polynomials are related to the polylogarithm

{Li}_{s} (z) = \sum_{k = 1}^{\infty} \frac{z^{k}}{k^{s}} .

For nonpositive integer values of s, the polylogarithm is a rational function. The first few are

${Li}_{0} (z) = \frac{z}{1 - z};$	${Li}_{- 1} (z) = \frac{z}{(1 - z)^{2}}$
${Li}_{- 2} (z) = \frac{z (1 + z)}{(1 - z)^{3}};$	${Li}_{- 3} (z) = \frac{z (1 + 4 z + z^{2})}{(1 - z)^{4}} .$

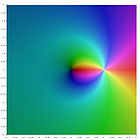
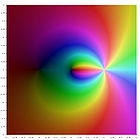
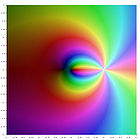
A plot of these functions in the complex plane is given in the gallery^[5] below.

**Polylogarithm functions in the complex plane**

${Li}_{0} (z)$	${Li}_{- 1} (z)$	${Li}_{- 2} (z)$	${Li}_{- 3} (z)$

In general the explicit formula for nonpositive integer s is

{Li}_{- n} (z) = \frac{z A_{n} (z)}{(1 - z)^{n + 1}} (n \geq 0) .

See also DLMF and the section on series representations of the polylogarithm on Wikipedia. However, note that the conventions on Wikipedia do not conform to the DLMF definition of the Eulerian polynomials.

Notes

↑ The Eulerian number $A_{n, k}$ is not to be confused with the value of the n^th Eulerian polynomial at k. For instance $A_{n, n} = 1, 0, 0, 0, \dots$ whereas $A_{n} (n)$ is A122778.
↑ Digital Library of Mathematical Functions, National Institute of Standards and Technology, Table 26.14.1
↑ The name Euler's triangle is used, for example, in Concrete Mathematics, Table 254. A virtue of this name is that it might evoke an association to Pascal's triangle, with which it shares the symmetry between left and right.
↑ Euler read his paper in the Königlichen Akademie der Wissenschaften zu Berlin in the year 1749 ("Lu en 1749"). It was published only much later in 1768.
↑ Author of the plots of the polylogarithm functions in the complex plane: Jan Homann. Public domain.

References

Leonhard Euler, Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques, 1768. E352 (Eneström Index), The Euler Archive.
Dominique Foata and Marcel-Paul Schützenberger, Théorie Géométrique des Polynômes Eulériens, 1970.
R. L. Graham, D. E. Knuth and O. Patashnik, Concrete Mathematics, 1989.
Friedrich Hirzebruch, Eulerian polynomials, Münster J. of Math. 1 (2008), 9–14.
Dominique Foata, Eulerian Polynomials: from Euler's Time to the Present. February 18, 2008.