|
 |
Eulerian polynomials
Peter Luschny, 2010−08−18
Contents |
Definition
The Eulerian polynomials are defined by the exponential generating function
The Eulerian polynomials can be computed by recurrence:
An equivalent way to write this definition is to set the Eulerian polynomials inductively by
The definition given is used by major authors like D. E. Knuth, D. Foata and F. Hirzebruch. In the older literature (for example in L. Comtet, Advanced Combinatorics) a slightly different definition is used, namely
Eulerian numbers
The coefficients of the Eulerian polynomials are the Eulerian numbers An,k [1],
This definition of the Eulerian numbers agrees with the combinatorial definition in the DLMF [2]. The triangle of Eulerian numbers is also called Euler's triangle [3].
|
|
Euler's definition An,k is A173018. The main entry for the Eulerian numbers in the database is A008292. It enumerates Cn,k with offset (1,1).
The combinatorial interpretation
Let Sn denote the set of all bijections (one-to-one and onto functions) from {1, 2, …, n} to itself, call an element of Sn a permutation p and identify it with the ordered list p1 p2 … pn.
Using the Iverson bracket [.] the number of ascents of p is defined as
where pn+1 ← 0. The combinatorial interpretation of the Eulerian polynomials is then given by
The table below illustrates this representation for the case n = 4.
| p | asc | p | asc | p | asc | p | asc |
| 4321 | 0 | 4231 | 1 | 2413 | 2 | 1423 | 2 |
| 3214 | 1 | 2431 | 1 | 2134 | 2 | 1342 | 2 |
| 3241 | 1 | 4312 | 1 | 2314 | 2 | 4123 | 2 |
| 3421 | 1 | 3142 | 1 | 2341 | 2 | 1324 | 2 |
| 4213 | 1 | 4132 | 1 | 3124 | 2 | 1243 | 2 |
| 2143 | 1 | 1432 | 1 | 3412 | 2 | 1234 | 3 |
The number of permutations of {1, 2, …, n} with n ascents (the central Eulerian numbers) are listed in A180056.
History

Eulerian polynomials in Institutiones calculi differentialis, 1755
Leonhard Euler introduced the polynomials in 1749 [4] in the form
Euler introduced the Eulerian polynomials in an attempt to evaluate the Dirichlet eta function
at s = -1, -2, -3,... . This led him to conjecture the functional equation of the eta function (which immediately implies the functional equation of the zeta function). Most simply put, the relation Euler was after was
Though Euler's reasoning was not rigorous by modern standards it was a milestone on the way to Riemann's proof of the functional equation of the zeta function.
The facsimile shows Eulerian polynomials as given by Euler in his work Institutiones calculi differentialis, 1755. It is interesting to note that the original definition of Euler coincides with the definition in the DLMF, 2010.
Eulerian generating functions
We call a generating function an Eulerian generating function iff it has the form
for some polynomial g(t). Many elementary classes of sequences have an Eulerian generating function. A few examples are collocated in the table below.
|
Generating function g(t)An(t)/(1-t)n+1 |
n = 0 | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 |
| g(t) = 1 − t2 | A019590 | A040000 | A008574 | A005897 | A008511 | A008512 |
| g(t) = 1 − t | A000007 | A000012 | A005408 | A003215 | A005917 | A022521 |
| g(t) = t | A057427 | A001477 | A000290 | A000578 | A000583 | A000584 |
| g(t) = 1 + t | A040000 | A005408 | A001844 | A005898 | A008514 | A008515 |
| g(t) = 1 + t + t2 | A158799 | A008486 | A005918 | A027602 | A160827 | A179995 |
For instance the case
- g(t) = t gives the generating function of the regular orthotopic numbers,
- g(t) = 1 + t gives the generating function of the centered orthotopic numbers.
Plot

|
A1(x) , A2(x) , A3(x) , A4(x) , A5(x) , A6(x) |
Special values of the Eulerian polynomials
| x | −1/2 | 1/2 | 3/2 |
| 2nAn(x) | A179929 | A000629 | A004123 |
| x | −2 | −1 | 0 |
| An(x) | A087674 | A155585 | A000012 |
| x | 1 | 2 | 3 |
| An(x) | A000142 | A000670 | A122704 |
Assorted sequences and formulas
Let ∂r denote the denominator of a rational number r.
| A122778 | An(n) |
| A180085 | An(−n) |
| A006519 | ∂(An(−1) / 2n) |
| A001511 | log2(∂(A2n+1(−1) / 22n+1)) |
Eulerian polynomials An(x) and Euler polynomials En(x) have a sequence of values in common (up
to a binary shift). Let Bn(x) denote the Bernoulli polynomials and ζ(n) the Riemann Zeta function.
 denotes the Stirling numbers of the second kind. The formulas below show how rich in content the Eulerian polynomials
are.
denotes the Stirling numbers of the second kind. The formulas below show how rich in content the Eulerian polynomials
are.
|
A155585 for all n ≥ 0 |
 |
 |
 |
 |
 |
 |
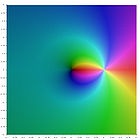
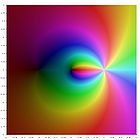
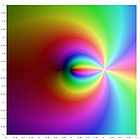
The connection with the polylogarithm
Eulerian polynomials are related to the polylogarithm
For nonpositive integer values of s, the polylogarithm is a rational function. The first few are
A plot of these functions in the complex plane is given in the gallery [5] below.
 |
 |
 |
 |
In general the explicit formula for nonpositive integer s is
See also DLMF and the section on series representations of the polylogarithm on Wikipedia. However, note that the conventions on Wikipedia do not conform to the DLMF definition of the Eulerian polynomials.
Program
- (Maple) a := proc(n,m) local k;
add((-1)^k*binomial(n+1,k)*(m+1-k)^n,k=0..m) end:
A := proc(n,x) local k; `if`(n=0,1,add(a(n,k)*x^k,k=0..n-1)) end:
Notes
- ↑ The Eulerian number An,k is not to be confused with the value of the nth Eulerian polynomial at k. For instance An,n = 1,0,0,0,... whereas An(n) isA122778.
- ↑ Digital Library of Mathematical Functions, National Institute of Standards and Technology, Table 26.14.1
- ↑ The name Euler's triangle is used, for example, in Concrete Mathematics, Table 254. A virtue of this name is that it might evoke an association to Pascal's triangle, with which it shares the symmetry between left and right.
- ↑ Euler read his paper in the Königlichen Akademie der Wissenschaften zu Berlin in the year 1749 ("Lu en 1749"). It was published only much later in 1768.
- ↑ Author of the plots of the polylogarithm functions in the complex plane: Jan Homann. Public domain.
References
- Leonhard Euler, Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques , 1768, E352 (Eneström Index).
- Dominique Foata and Marcel-Paul Schützenberger, Théorie Géométrique des Polynômes Eulériens, 1970.
- R. L. Graham, D. E. Knuth and O. Patashnik, Concrete Mathematics, 1989.
- Friedrich Hirzebruch, Eulerian polynomials, Münster J. of Math. 1 (2008), 9–14.
- Dominique Foata, Eulerian Polynomials: from Euler's Time to the Present. February 18, 2008.
This article was originally written for the OeisWiki. Thanks to Daniel Forgues for editorial help. It is also available in pdf format.