The Bernoulli numbers are the children of the zeta function ...
The Bernoulli Manifesto
A survey on the occasion of the 300-th anniversary of the publication of
Jacob Bernoulli's Ars Conjectandi, 1713-2013.
Avant-propos: The starting point of this public letter was a discussion in the Newsgroup de.sci.mathematik. The central question was: Are the Bernoulli numbers misdefined? I presented the question in an open letter to Donald E. Knuth. Professor Knuth was kind enough to respond. Below is my response to Prof. Knuth. In order to understand this response the reading of the previous correspondence is recommended.
The generating function approach
Dear Professor Knuth,
Thank you for taking the time to respond to my letter.
You seem to prefer the generating function $ze^{z}/(e^{z}-1)$ instead of $z/(e^{z}-1)$;
Yes and no. My primary concern is to find a substantive definition of the Bernoulli numbers. A definition that, if it is to be, even goes beyond the paradigmatic example given by Bernoulli himself and embeds naturally into the wider field of mathematics. Only then would I like to turn to the question of representations. And a generating function is a formal representation, that serves, first and foremost, simple computational manipulation of these numbers, but which should always remain subordinate to their content and never reach the rank of a substantive definition.
But to comply with the course of the discussion we will put the cart before the horse. What we can immediately agree upon is the generating function of the Bernoulli polynomials.
\begin{equation} \frac{ze^{zx}}{e^{z}-1}=\sum \limits_{n=0}^{\infty}B_{n}(x)\frac{z^{n}}{n!} \ . \ \label{BP} \end{equation}Taking this as the point of departure, only two things now come into consideration to be called Bernoulli numbers: the coefficients which result from inserting $x=0$ or $x=1$ into the generating function (\ref{BP}).
\begin{align} B^{(0)}(z) & = \frac{z}{e^{z}-1} \ = \, {\textstyle\sum\limits_{n=0}^{\infty}} B_{n}(0)\frac{z^{n}}{n!}\ \label{B0} \\[4pt] B^{(1)}(z) & = \frac{z}{1-e^{-z}} = % = \frac{ze^{z}}{e^{z}-1} {\textstyle\sum\limits_{n=0}^{\infty}} B_{n}(1)\frac{z^{n}}{n!}\ \label{B1} \end{align}So the question is which of the two sequences
\begin{align} B_{n}(0) & = 1,-\frac{1}{2},\frac{1}{6},0,-\frac{1}{30},0,\frac{1}{42}, \ldots \\[4pt] B_{n}(1) & = 1,+\frac{1}{2},\frac{1}{6},0,-\frac{1}{30},0,\frac{1}{42}, \ldots \end{align}is more likely to represent the unity of mathematics (in the sense of B. Mazur's essay Bernoulli numbers and the unity of mathematics).
Indeed, these two sequences differ only for $n = 1$ and also only because of the sign $B_{1}(1)=-B_{1}(0).$ This is an unfortunate coincidence because it tends to belittle what is no bagatelle. To say that the sum of the coefficients of a polynomial has a certain value is a much more substantial statement than to give a name to its constant term.
Bernoulli numbers and Stirling polynomials.
… but I can think of many reasons to prefer the latter formula ... not least the connection with Stirling numbers in Concrete Math (7.52), although I realize that the former function does arise in my definition of Stirling polynomials in Concrete Math (6.50).
Let us consider
\begin{equation} \left(B^{(1)}(z)\right)^{x} = x\sum_{n\geq0}\sigma_{n}(x)z^{n}\ . \end{equation}You define the Stirling polynomials $\sigma_{n}$ based on $B^{(1)}(z),$ and this makes sense to me as thereby the relationship between Stirling polynomials and Bernoulli numbers can be easily expressed provided one sets $\operatorname{B}_{n} = B_{n}(1)$.
\begin{equation} n!\sigma_{n}(1)=B_{n}(1) \quad(n\geq0) \ . \label{SPB} \end{equation}
With this choice $\left(B^{(1)}(z)\right)^{m}$ for $m=1$ directly represents the relationship between the Stirling polynomials and the Bernoulli numbers. A simpler and more coherent relationship cannot be expected.
Let us now consider the counterpart, the relation between $\sigma_{n}(0)$ and $B_{n}(0).$ It turns out a lot more problematic. In Concrete Math Exercise 6:18 we find the identity
\begin{equation} (x+1)\sigma_{n}(x+1)=(x-n)\sigma_{n}(x)+x\sigma_{n-1}(x)\ . \label{stirpoly} \end{equation}Substituting $x=0$ we obtain $\sigma_{n}(1) = -n \sigma_{n}(0)$. If we choose $n = 0$ then an arithmetical exception occurs because $\sigma_{0}(x) = 1/x$. Therefore $\sigma_{0}(0)$ can not be $B_{0}(0)$. If we choose $n = 1$ then unfortunately $1/2=-1/2$ follows since $\sigma_{1}(x)=1/2.$ Thus obviously the choice $\operatorname{B}_{n} = B_{n}(0)$ has to be avoided here.
In summary: If one chooses the definition $\operatorname{B}_{n}=B_{n}(1),$ one can take instead of
| Concrete Math (7.44) | $\frac{z}{e^{z}-1}$ | the expression $\ B^{(1)}(z)$, |
| Concrete Math (7.52) | $\frac{z}{1-e^{-z}}$ | the expression $\ B^{(1)}(z)$, |
| Concrete Math (6.50) | $\frac{ze^{z}}{e^{z}-1}$ | the expression $\ B^{(1)}(z)$. |
This describes the connection between the Bernoulli numbers and the Stirling polynomials more clearly and uniformly.
If we understand the search for the true Bernoulli numbers as a match, then identity $ (\ref{SPB}) $ scores $\mathbf{1:0}$ for the choice $\operatorname{B}_{n}=B_{n}(1).$
The Bernoulli function.
Now let's look at the Bernoulli function $\mathcal{B}(s)$. We write $ \tau = 2 \pi$.
\begin{equation} \mathcal{B}(s)=-2\cos(s\tau/4)s!\,\zeta(s)/\tau^s \label{berfun} \end{equation}
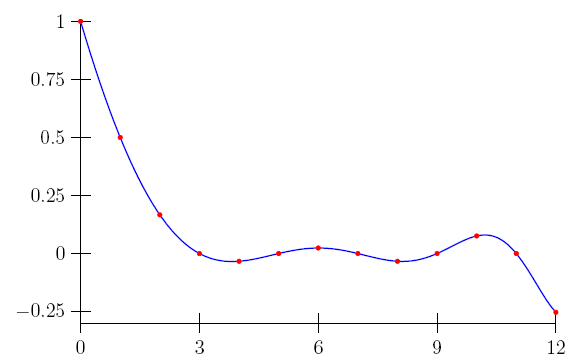
The real Bernoulli function $\mathcal{B}(s)=-s\zeta(1-s)$
… notice that there are many functions that interpolate the Bernoulli numbers at all positive integers; for example, multiply your `Bernoulli function' by $e^{2\pi is}$ or by $\cos\pi s$.
Yes of course, there are also infinitely many functions which interpolate the numbers $1,1\cdot2,1\cdot2\cdot3,1\cdot2\cdot3\cdot4,…$. Yet no one will come up with the idea to glue a cosine factor onto the $\Gamma$ function found by Daniel Bernoulli and Leonhard Euler. And neither here. Of course it is true that, if we consider $\mathcal{B}(s)\cos(\pi s)$, we could hit $-1/2$ at the point $1$ by adding a few meaningless oscillations.
But for heaven's sake, our definition is not chosen arbitrarily! The value of the definition lies in the connection with the Riemannian functional equation. In fact it is almost identical to its right hand side!
\begin{equation} \zeta(1-s) = 2\cos(s\tau/4)\,\Gamma(s)\,\zeta(s)/\tau^s \label{Z} \end{equation}Using it we get the representation
\begin{equation} \mathcal{B}(s)=-s\zeta(1-s) \ . \label{BZ} \end{equation}
We introduce here basically a convenient notation which helps us to reap the fruits of the Riemann functional equation in the context of the Bernoulli numbers. The functional equation must stay intact of course.
This approach can be continued to the representation of the Bernoulli polynomials by the Hurwitz zeta function.
\begin{equation} \zeta\left(-n,w\right) =-\frac{B_{n+1}(w)}{n+1}\qquad\left(n\geq0\right) \end{equation}This is explained, for instance, in T. Apostol, Introduction to Analytic Number Theory, (th. 12.13 and 12.16). Setting $w=1$ we get
\begin{equation} B_{n}(1)=-n\zeta(1-n) \ . \label{bezeta} \end{equation}
Thus the Bernoulli function is exactly the confluent continuation of this identity. The cases $n=0$ and $n=1$ still require special consideration. In these cases $\mathcal{B}(n)=\lim_{t\rightarrow n}\mathcal{B}(t)$ is to be understood. But both limits exist, $\lim_{t\rightarrow0}\mathcal{B}(t)=1$ and $\lim_{t\rightarrow1}\mathcal{B}(t)=1/2$. So once we have introduced the Bernoulli function $\mathcal{B}(s)$ it makes sense to define $\operatorname{B}_{n}=\mathcal{B}(n)$. And since
\begin{equation} \mathcal{B}(n)=B_{n}(1) \end{equation}
the score is $\mathbf{2:0}$ for the choice $\operatorname{B}_{n}=B_{n}(1).$ Only this choice correctly reflects the connection with the zeta function.
However in contrast to the $\zeta$ function the Bernoulli function does not have a pole at $s=1$. This fact makes it possible to determine the value of $\operatorname {B}_{1}$ without having to rely on conventions.
A more satisfying way to introduce the Bernoulli function directly without reference to the the $ \zeta $ function and its disruptive pole will be described below. It generalizes a representation of the Bernoulli numbers due to J. Worpitzky and was given by Helmut Hasse in 1930.
 |
 |
The continuation of an almost miraculous formula.
Consider the following beautiful formula
\begin{equation} \frac{\tau^{s}\mathcal{B}(s)}{s!}=-2\cos(s\tau/4)\,\zeta(s) \ \label{R} \end{equation}($ \tau = 2 \pi$), which is valid for all complex numbers if the function is continued in the points $\left\{0,1\right\}$ by the respective limits. In particular we have
\begin{equation} \frac{\tau^{n}\operatorname{B}_{n}}{n!}=-2\cos(n\tau/4)\,\zeta(n)\quad (n \gt 1 \ \text{integer})\ . \end{equation}Substituting in this formula $\operatorname{B}_{1}=1/2$ we obtain $\pi=\pi$, but substituting $\operatorname{B}_{1}=-1/2$ we obtain $-\pi=\pi$.
Comparing (\ref{R}) with Concrete Math (6.89), a formula of Euler that you called an almost miraculous closed form for infinitely many infinite sums,
\begin{equation} \frac{\tau^{2n}B_{2n}(0)}{ \left( 2n \right) !} = -2(-1)^{n}\zeta(2n) \qquad(n \gt 0) \label{E} \end{equation}one sees that (\ref{E}) is nothing other than the precursor of (\ref{R}), which in turn is nothing else than the Riemann functional equation (\ref{Z})!
And (\ref{E}) is almost miraculous while (\ref{R}) might get a cosine factor attached? This is not possible. Setting $\operatorname{B}_{1}=B_{1}(0)$ would compromise this highlight of mathematics and its history by implying $-\pi=\pi$. Match score $\mathbf{3:0}$ for the choice $\operatorname{B}_{n}=B_{n}(1)$ because it does not lead to such absurd consequences.

An almost miraculous function, $-\tau^{s}\zeta(1-s)/(s-1)!$
The functional equation of the Bernoulli function.
Since $2 \cos(\pi s / 2) = i^s + (-i)^s $ and using the notation $\tau = 2 \pi$ equation $(\ref{R})$ can also be written as
\begin{equation} \mathcal{B}(s) = - {s!} \ \zeta(s) \frac{i^s + (-i)^s }{\tau^s} . \label{bertau} \end{equation}
Furthermore, because of $(\ref{BZ})$ $ \mathcal{B}(1-s) = (s-1) \zeta(s) $ we obtain a self-referential representation of the $\mathcal{B}$ function
\begin{equation} \mathcal{B}(s) = s! \, \frac{\mathcal{B}(1-s)}{1-s} \frac{i^s + (-i)^s }{\tau^s} . \end{equation}
The miraculous formula emerged as a functional equation of the Bernoulli function! This functional equation has also a symmetric variant like its $\zeta-$cousin:
\begin{equation} \left( \frac{s}{2} \right) ! \ \pi^{-s/2} \ \mathcal{B}(1-s) = \left( \frac{1-s}{2} \right)! \ \pi^{-(1-s)/2} \ \mathcal{B}(s) \label{symfe} \end{equation}
This means that the function on the left side of $(\ref{symfe}) $ is unchanged by the substitution $s \leftarrow 1-s .$
 |
 |
Some assorted facts about the Bernoulli function
The Bernoulli function doesn't have any zero on the left of $\Re(s) = \sigma = 0$ (nor on the line $\sigma = 0$ — a fact which is indeed equivalent to the prime number theorem). The zeros split into those with $\Im(\rho) = 0$ and $\Im(\rho) \neq 0.$ According to the Riemann Hypothesis the latter all lie on the line $\sigma = 1/2.$
For those who try to find a counterexample to the Riemann hypotheses the Bernoulli function is a suitable tool because the Bernoulli function has the same zeros as the zeta function on this critical line. This follows from a fact discovered by Riemann: if $\rho$ is a zero of the Riemann zeta function then so is $1−\rho$.

The zeta and the Bernoulli function on the critical line.
The series expansion of $\mathcal{B}(s)$ follows from the Laurent series expansion of the Riemann zeta function
\begin{equation} 1 - \gamma s - \gamma_1 s^2 - \frac{\gamma_2 }{2}s^3 - \frac{\gamma_3 }{6} s^4 + O(s^5) \end{equation}where $\gamma$ is the Euler-Mascheroni constant and $\gamma_n$ is the n-th Stieltjes constant. This fact can be used to define the Stieltjes constants as the coefficients of this expansion of the Bernoulli function. This definition is simpler than the definition usually given, namely as constants that occur in the Laurent series expansion of the Riemann zeta function.
Thus we can write
\begin{equation} \operatorname{B}(s) \, = \, 1 - s \sum_{n \ge 0} \, \gamma_n \frac{s^n}{n!}. \end{equation}For the controversial case $s=1$ we find $\operatorname{B}_{1} =1 - 1/2$ because it is well known that $\sum_{n \ge 0} \gamma_n / n! = 1/2$. This fact raises the score to $\mathbf{4:0}$ for the choice $\operatorname{B}_{n}=B_{n}(1).$
If we use the generalized Stieltjes constants $\gamma_n(a)$ instead of the ordinary ones we arrive at the generalized Bernoulli function $\operatorname{B}(s,a)$, which is a generalization analogous to the generalization of the Riemann Zeta function to the Hurwitz Zeta function.
The Euler-MacLaurin summation can be used to prove the formula
\begin{equation} - \frac{\mathcal{B}'(0)}{\mathcal{B}(0)} = \gamma. \end{equation}This means that $- \gamma$ is the slope of the tangent line of the Bernoulli function at the origin — like the slope of the factorial function at this point! Julian Havil would be delighted.
This makes one curious to gain more information about the function ${- \mathcal{B}'(s)}/{\mathcal{B}(s)}$, which can be written in terms of the zeta function as
\begin{equation} - \frac{\mathcal{B}'(s)}{\mathcal{B}(s)} = \frac{\zeta'(1-s)}{\zeta(1-s)} - \frac{1}{s}, \qquad (s \neq 0). \end{equation}Lastly we mention that in the interval $-2 \le s \le 1 $ \begin{equation} \mathcal{B}(1-s) \approx \frac{1}{2} + \frac{5}{12}s + \frac{1}{12} s^2 \end{equation} is a fairly good first approximation as can be seen from the Euler-MacLaurin expansion of the $\zeta$ function. The approximation is exact for $ s \in \{ -2, -1, 0, 1 \}.$ We will return to the Euler-MacLaurin expansion of the $\zeta -$ function below.

The function $- \frac{\mathcal{B}'(s)}{\mathcal{B}(s)}$ hits Euler's $\gamma$ at $s=0.$
The Hadamard product of the Bernoulli function.
The Bernoulli function can be written as a product $\mathcal{B}(s) = T(s)R(s)$ where $T(s)$ takes care of the zeros with $\Im(\rho) = 0$ and $R(s)$ for those with $\Im(\rho) \neq 0.$ (We will call $T(s)$ the trivial part and $R(s)$ the Riemann part of the Bernoulli function.)
Let $ \gamma$ be Euler's constant and $ t = s/2-1/2$ then $T(s)$ is defined as
\begin{equation} T(s) = \sin(\pi t)\, \Gamma(t)\, e^{(2+\gamma)t } (2 \pi)^{-s}. \end{equation}$T(s)$ can be seen as a first approximation to the Bernoulli function which computes all values at odd integers exactly. The formula clearly displays the zeros at 3, 5, 7, ... (the vanishing of the Bernoulli numbers at these indices) due to the sine function term but also gives the value of $\mathcal{B}(1) = 1/2$ (understood as a limit).
The second function, $R(s)$, is quite a delicate function which Hadamard derived from the Weierstrass factorization theorem. It is a product over the zeros $\rho$ of the Riemann zeta function with $\Im(\rho) \neq 0$.
\begin{equation} \mathcal{B}(s) = T(s) \prod_{\rho} \left(1-\frac{s}{\rho}\right) \exp \left( \frac{s}{\rho} \right) \qquad (s \gt 0) \end{equation}
The plot below shows the Bernoulli function, the trivial part of the Bernoulli function and an approximation using the Weierstrass factorization theorem where the product is taken over the first one hundred zeros of the zeta function.

The Hadamard factorization of the Bernoulli function
The fact that Weierstrass and Hadamard voted (implicitly) for $\mathcal{B}(1) = 1/2$ raises the match score to $\mathbf{5:0}$. Yet there is a second, simpler form of the factorization formula which highlights the value of the Bernoulli function at $s=1$ in a striking fashion.
\begin{equation} \mathcal{B}(s) = \frac{1}{2} \frac{\pi^{1/2-s/2}}{(1/2-s/2)!} \prod_{\rho} \left(1-\frac{s}{\rho}\right) \end{equation}
The alternating Bernoulli function.
The alternating Riemann zeta function is defined as $\zeta^{*}(s) = \zeta(s)(1- 2^{(1-s)}).$ The alternating Bernoulli function has the same definition as the Bernoulli function except that the zeta function is replaced by the alternating zeta function.
\begin{equation} \mathcal{B}^{*}(s) = -s \zeta^{*}(1-s). \label{betastardef} \end{equation}
For $s=0$ the right side of $(\ref{betastardef})$ is understood as a limit, $ \mathcal{B}^{*}(s) =$ $ \lim_{s \rightarrow 0} -s \zeta^{*}(1-s) $ $ = 0.$ In terms of the Bernoulli function the definition can be restated as
\begin{equation} \mathcal{B}^{*}(s) = \mathcal{B}(s) \left( 1-2^{s} \right). \label{betastar} \end{equation}Using equation $(\ref{bertau})$ we can also express the alternating Bernoulli numbers in terms of the zeta function (using the notation $\tau = 2 \pi$)
\begin{equation} \mathcal{B}^{*}(s) = {s!}\ \zeta(s) \left(2^{s} -1 \right)\frac{ i^s + (-i)^s }{\tau^s} . \end{equation}
Introducing the function $z_t(s) =(i/ ( t \pi))^s + (-i/(t \pi))^s$ we have the alternate form
\begin{equation} \frac{\mathcal{B}^{*}(s)}{s!} = \zeta(s) ( z_1(s)- z_2(s)). \end{equation}
The alternating Bernoulli numbers.
The alternating Bernoulli numbers are the values of the alternating Bernoulli function at the nonnegative integers.
\begin{equation} \operatorname{B}^{*}_n = \mathcal{B}^{*}(n). \end{equation}Like the Bernoulli numbers the alternating Bernoulli numbers are rational numbers. A distinctive feature characterizes them: reduced to lowest terms they all have the same denominator, which is $2$. Thus it is convenient to introduce the integers $\operatorname{G}_n = 2 \operatorname{B}^{*}_n .$ These numbers are known as the Genocchi numbers.
\begin{equation} \operatorname{G}_n \, = \, 0,\,−1,\,−1,\,0,\,1,\,0,\,−3,\,0,\,17,\,0,\,−155,\,0,\,2073, \ldots \quad (n \ge 0) \end{equation}

The Genocchi function $2 \mathcal{B}^{*}(x) = 2x\zeta(1-x)(2^x-1)$
It should be noted that our approach introducing the Genocchi numbers as $ \operatorname{G}_n = 2 \mathcal{B}^{*}(n) $ defines the numbers for all $ n \ge 0$, unambiguously also in the case $n=1$.
If we did not have the Bernoulli function as a fixed reference we would have to start another meaningless Glasperlenspiel (glass bead game) with generating functions, just running once again into similar problems as with the Bernoulli numbers. We would have to ask ourselves: is $2x/(1+e^x)$ or is $-2x/(1+e^{-x})$ the exponential generating function? Is $\operatorname{G}_1 = 1$ or $\operatorname{G}_1 = -1$? Match score $\mathbf{6:0}$.
Herbert Wilf's famous dictum "A generating function is a clothesline on which we hang up a sequence of numbers for display" clearly implies that we first have to have the clothes which we wish to hang up — a simple fact often forgotten by users of generatingfunctionology.
The Euler-MacLaurin expansion of the Riemann zeta function.
The way the relationship between finite and infinite calculus is described in Concrete Math (2.6) also serves to illuminate the relationship between the zeta function and the Bernoulli numbers. So let
\[ \zeta(s)=\lim_{N\rightarrow\infty}\sum_{n=1}^{N} \frac{1}{n^s} \]If we expand analytically using the Euler-MacLaurin formula we find with $\operatorname{B}_{n}= B_{n}(1)$
\begin{equation} \zeta(s)=\sum_{k=0}^{K}\frac{\operatorname{B}_{k}}{k!}s^{\overline{k-1}} + R(s,K) \ . \label{aztaknu} \end{equation}
$R(s,K)$ denotes a remainder term which is of no further interest here. The point is the closed form of the sum. Written explicitly:
\begin{align} \zeta(s) & = \frac{\operatorname{B}_{0}}{0!}s^{\overline{-1}}+\frac{\operatorname{B} _{1}}{1!}s^{\overline{0}}+\frac{\operatorname{B}_{2}}{2!}s^{\overline{1}} +\cdots+R(s,K)\nonumber\\ & = \frac{1}{s-1}+\frac{1}{2}+\frac{1}{12}s+\cdots+R(s,K) \nonumber \ . \end{align}The Euler-MacLaurin formula, the calculation rules of rising powers, the Bernoulli numbers, everything blends in beautifully, as long as we select $\operatorname{B}_{1}=1/2$, and not $-1/2$. Match score $\mathbf{7:0}.$
And what about the practice? I pick out an example from a paper in the arXiv. It illustrates a situation which is typical for a whole class of Euler-MacLaurin expansions which by setting $\operatorname{B}_{1}=-1/2$ lose in formal content. The author gives the above expansion of the zeta function like this:
\begin{equation} \zeta(s)=\frac{1}{s-1}+\frac{1}{2}+\sum_{k=1}^{K}\frac{\operatorname{B}_{2k}}{(2k)!} s(s+1)\cdots(s+2k-2)+R(s,K) \label{zetaexpl} \end{equation}The clear and succinct formula (\ref{aztaknu}) has become a formulae mish-mash whose true structure still has to be reconstructed.
But the author (\ref{zetaexpl}) was virtually forced to choose the elaborated form, because only this allowed him to write $\operatorname{B}_{1}=1/2$ without coming into conflict with the convention $\operatorname{B}_{1}=-1/2$.
We see how the wrong choice of $\ \operatorname{B}_{1}$ can lead to a considerable loss of formal conciseness.
The correct indexing of sums.
Dijkstra correctly said that most loops should run from 0 to n - 1, not from 1 to n. That's why the sum of \[ 0^{m}+1^{m}+\cdots+(n-1)^{m} \] is cleaner (and more satisfying to a mature mathematician) than $1^{m}+\cdots+n^{m}$.
Agreed! But such a representation is with $\operatorname{B}_{1}=1/2$ just as possible as with $\operatorname{B}_{1}=-1/2$:
\begin{align*} {\textstyle\sum\limits_{k=0}^{n-1}}k^{m} & =\frac{1}{n+1}(B_{n+1}(m)-B_{n+1}(0))\ ,\\ {\textstyle\sum\limits_{k=0}^{n-1}} k^{m} & =\frac{1}{n+1}(B_{n+1}(m)-(-1)^{n+1}B_{n+1}(1)) \ . \end{align*}As such, this point is not relevant to this discussion.
Harmonic sum
But we will take up the advice. The harmonic sum is one of the recurring themes of Concrete Math. Let us consider formula (9.88), which is for $n\geq1$
\begin{equation} \sum_{k=1}^{n}\frac{1}{k}=\ln(n)+\gamma+\frac{1}{2n}-\sum_{k=1}^{m} \frac{B_{2k}(0)}{2kn^{2k}}+R(2m,n)\ . \label{HMS1} \end{equation}We counter with the formula $(n\geq1)$
\begin{equation} \sum_{k=0}^{n-1}\frac{1}{k+1}=\ln(n+1)+\gamma-\sum_{k=1}^{m} \frac{B_{k}(1)}{k}(n+1)^{-k}+\tilde{R}(m,n)\;. \label{harm2} \end{equation}First we note that both formulas provide the same: they approximate $H_{n}$, the $n$-th harmonic number, the second formula slightly better than the first. The right side of the second formula is shorter, the term $1/(2n)$ has disappeared, arguably it is more elegant and memorable.
What does this example teach us? It's worthwhile to follow the advice of Dijkstra and Knuth — but we always knew this — here about the correct way to index the sum on the left side of $(\ref{harm2}).$ But what happens if we were to write $B_{k}(0)$ on the right side of $(\ref{harm2})$? This neat formula would be broken!
Bernoulli numbers and harmonic numbers.
It seems natural to mention next a representation of the Bernoulli numbers by the harmonic numbers.
\begin{equation} \operatorname{B}_{n} = \sum_{k=0}^n \sum_{v=0}^k (-1)^v \binom{k}{v} H_{k+1}(v+2)^n \ . \label{harm} \end{equation}I like this relationship well enough to award a point for it. This leads to the match score $\mathbf{8:0}$ as the right side of $(\ref{harm})$ reduces to $1/2$ in the case $n=1$.
This formula is the special case $x=1$ of the following representation of the Bernoulli polynomials:
\begin{equation} B_{n}(x) = \sum_{k=0}^n \sum_{v=0}^k (-1)^v \binom{k}{v} H_{k+1}(x+v+1)^n \end{equation}Further remarks and generalizations of these identities can be found on my blog Zeta Polynomials and Harmonic Numbers.
Does the choice $B_1=1/2$ break widely-used formulas?
On the other hand the choice $B_{1}=1/2$ in our last example does not affect the first formula since the sum on the right side of $(\ref{HMS1})$ runs only over the even Bernoulli numbers. This observation is typical. One does not need to be afraid that classical formulas like the expansions of special functions, such as given for example in the Handbook of Mathematical Functions (HMF) or the Table of Integrals, Series and Products of I. S. Gradshteyn and I. M. Ryzhik would be affected by using $\operatorname{B}_{k} = B_{k}(1)$ and thus introduce confusion. This is not the case. A review of the relevant chapters of these two reference books shows that $\operatorname{B}_{1} $ is not used there but only the Bernoulli numbers at even indices.

Some function expansions in the typical cluttered $\operatorname{B}_{2k}$
style
(from H. Cohen, Number Theory)
In the first pages of Concrete Math you explain techniques that make summation user-friendly and comment that the omission of terms in a sum is not always a good idea:
But such temptations should be resisted; efficiency of computation is not the same as efficiency of understanding!
... and readability of formulas, one might add. Why can't the mathematicians trusted to remember the fact $\operatorname{B}_{k} = 0 $ for odd $k\gt1$ when they really need it? Instead all this clutter!
Moreover the use of $\operatorname{B}_{k} = B_{k}(1)$ could have lead to simpler formulas also in the HMF, for example in (6.3.18) or (6.4.11). The classical Poincaré-type asymptotic expansion of the digamma function then could simply and concisely be written:
\begin{equation} \psi(z) \sim \ln z - \sum_{k=1}^{\infty} \frac{\operatorname{B}_{k}}{k z^k} \label{digam} \end{equation}
This formula raises the match score to $\mathbf{9:0}$ and we note that $\operatorname{B}_{k} = B_{k}(1)$ gives us more freedom in the design of formulas.
Non-natural ranges of validity.
The observation that some identities have a smaller and non-natural range of validity if one chooses $B^{(0)}(z)$ instead of $B^{(1)}(z)$ strikes me as a more serious problem. This is a sensitive seismograph indicating that some deeper tectonic layers are in conflict.
Let us denote the Euler numbers by $E_{n}$ and consider the following identity
\begin{equation} \operatorname{B}_{n}=\genfrac{.}{.}{}{}{n}{4^{n}-2^{n}} \sum_{k=0}^{n-1} \binom{n-1}kE_{k} \ . \label{BE1} \end{equation}The choice of $B^{(1)}(z)$ includes the case $n=1$ while the choice $B^{(0)}(z)$ precludes this case although no plausible reason suggests this.
For many authors, however, this is not enough. If the index $n=1$ is dropped, they exclude also all other odd $n$ from the sum. The result is the following disaster (dlmf.nist.gov/BP.4.15)
\begin{equation} \operatorname{B}_{2n}=\genfrac{.}{.}{}{}{2n}{2^{2n}(2^{2n}-1)} \sum_{k=0}^{n-1}\binom{2n-1}{2k}E_{2k} \ . \label{BE2} \end{equation}What was once a simple formula $(\ref{BE1}) $ valid with $B^{(1)}(z)$ for all $n \gt 0$ now is a formula with a bloated notation $(\ref{BE2})$ and half as much content.
Bernoulli numbers and Eulerian numbers.
Another non-natural limitation of the scope of validity can be observed when we look at the important connection between the Bernoulli numbers and the Eulerian numbers $ \genfrac <> {0pt}{}{n}{k} $ (OEIS A173018, the Concrete Math version), which is given by the following two formulas:
\begin{equation} \sum_{k=0}^n (-1)^k \genfrac <> {0pt}{}{n}{k} = \frac{4^{n+1}-2^{n+1}}{n+1} B_{n+1}, \end{equation} \begin{equation} \sum_{k=0}^n (-1)^k \genfrac <> {0pt}{}{n}{k} {\binom{n}{k}}^{-1} = (n+1) B_n. \end{equation}Both formulas are valid for $n \ge 0$ if we set $\operatorname{B}_{1} = 1/2$. Conversely, if we set $\operatorname{B}_{1} = -1/2$ then they are only valid for $n \ge 1$ and $n \ge 2$, respectively. Clearly the wrong definitions of the Bernoulli numbers limit our understanding of the situation and are a potential source of errors. This leads to the match score $\mathbf{10:0}$.
However, the most important relation between Bernoulli numbers and Eulerian numbers, assuming $\operatorname{B}_n = \operatorname{B}_n(1)$, is
\begin{equation} \operatorname{B}_n = \sum_{k=0}^n\frac{(-1)^k}{k+1} \sum_{j=0}^k \genfrac <>{0pt}{}{n}{j} \binom{n-j}{n-k}. \end{equation}
The reason is the identity
\begin{equation} (-1)^k \sum_{j=0}^k \genfrac <>{0pt}{}{n}{j} \binom{n-j}{n-k} = {\sum\limits_{j=0}^{k}}(-1)^{j}\binom{k}{j}\left(j+1\right)^{n} \ . \label{berulerian} \end{equation}
These are the Worpitzky numbers and we will meet them again under the name $\Delta^{k}\left({n}\right)$ in the analytic definition of the Bernoulli numbers below.
To round off these remarks: If we set $\operatorname{B}_n = \operatorname{B}_n(1)$ and let $A_n(x)$ denote the Eulerian polynomials, $E_n(x)$ the Euler polynomials and $\genfrac\{\}{0pt}{}{n}{k} $ the Stirling subset numbers, then the Bernoulli numbers also have their place in this remarkable chain of identities:
| $ A_{n}(-1) $ |
| $ = E_{n}(1) 2^n $ |
| $ = \zeta(-n)(2^{n+1}-4^{n+1}) $ |
| $ = \operatorname{B}_{n+1} \frac{4^{n+1}-2^{n+1}}{n+1} $ |
| $ = \sum_{k=0}^n \genfrac\{\}{0pt}{}{n}{k} (-2)^{n-k} k! $ |
| $ = \sum_{k=0}^n \sum_{v=0}^k \binom{k}{v} (-1)^v 2^{n-k}(v+1)^n $ |
Two identities.
Consider, for example, the fact that \begin{equation} z/(e^{z}-1)-z/(e^{z}+1)=2z/(e^{2z}-1)\ , \label{identity1} \end{equation} an identity with many more applications …
I'm not sure if I understand the meaning of this remark properly. If you feel that the existence of the identity $(\ref{identity1})$ is an argument in favor of the choice of the generating function $B^{(0)}(z)$, then I would point out that an identity of no less beauty exists which would then argue in favor of the choice of $B^{(1)}(z)$. Since
\begin{equation} B^{(1)}(z)=ze^{z}/(e^{z}-1)=z/(1-e^{-z}) \end{equation}we are led by analogy to $(\ref{identity1})$ to the identity
\begin{equation} z/(1-e^{-z})-z/(1+e^{-z})=2z/(e^{z}-e^{-z})\ . \label{identity2} \end{equation}The identity $(\ref{identity2})$ does not change under the substitution $z \leftarrow -z$. Thus it can be written equivalently
\begin{equation} z/(1+e^{z}) - z/(1-e^{z}) =2z/(e^{z}-e^{-z})\ . \end{equation}
Topology and the Todd function.
Your last comment prompted me to reconsider the two rivaling generating functions $(\ref{B0})$ and $(\ref{B1})$ and to ask if there is something special which characterizes one of the two. And indeed there is:
Let $f(z)$ be a power series with constant term 1 such that the coefficient of $x^n$ in $(f(x))^{n+1}$ equals 1 for all n. (*)
As it has been observed by Friedrich Hirzebruch (Prospects in Mathematics, AM-70), $f(z) = z/(1-e^{-z})$ is the only power series satisfying (*). This function is called the Todd function (after John Arthur Todd).
Here we see the Bernoulli numbers show up in topology. Thus if we accept $B_1 = 1/2$ we can state: The Todd function is the exponential generating function of the Bernoulli numbers. And we can simply write
\[ \frac{z}{1-e^{-z}} = \sum_{k \ge 0} B_k \frac{x^k}{k!}. \]As we said in the introduction, before fixing the meaning of the Bernoulli numbers for the case $n=1$ it is a good idea to look not only at the paradigmatic case discussed by Bernoulli himself. Since the Todd class (defined by the Todd function) plays a fundamental role in the generalization of the theorem of Riemann-Roch for higher dimensions and in similar topological theorems we regard this as an strong argument in favor of $B_{1}=1/2$ and set the match score to $\mathbf{11:0}$.
Von Staudt! Clausen! To the rescue!
|
|
Assume that the small table above is presented to you and you are asked to make a suggestion, spontaneous and intuitive, for the value of $\operatorname{B}_{1}.$ What would you say? $-1/2$? How would you justify that? Only $ 1-1/2 $ comes to my mind. Admittedly this is not an argument.
However, two grand masters of the Bernoulli numbers, von Staudt and Clausen, have already answered the question back in 1840 when they independently found how the denominators of the $\operatorname{B}_{n}$ can be understood; their now famous theorem is only the phrasing of the above table in general terms.
I find this observation pretty enough to award a point for it. Match score $\mathbf{12:0}$ for von Staudt's and Clausen's voting for $\operatorname{B}_{n}=B_{n}(1).$
The fabolous Fubini polynomials.
Let $n\brace k $ denote the Stirling set numbers. The Fubini polynomials are defined as $\operatorname{F}_n(x) = \sum_{k=0}^n (-1)^{n-k} k! \genfrac\{\}{0pt}{}{n}{k} x^k $ (see OEIS A278075).

Note that for all $n \ge 1 \ $ $\operatorname{F}_n(0) = 0$ and $\operatorname{F}_n(1) = 1$. The Fubini polynomials have the remarkable property that $\int_{0}^{1} \operatorname{F}_n(x) \, dx = \operatorname{B_n}. $
| $\int_{0}^{1}\ 1 \ dx = 1$ |
| $\int_{0}^{1}\ x \ dx = \frac12$ |
| $\int_{0}^{1}\ (2 x^2 - x) \ dx = \frac16$ |
| $\int_{0}^{1}\ (6 x^3 - 6 x^2 + x) \ dx = 0$ |
| $\int_{0}^{1}\ (24 x^4 - 36 x^3 + 14 x^2 - x) \ dx = -\frac{1}{30}$ |
| $\int_{0}^{1}\ (120 x^5 - 240 x^4 + 150 x^3 - 30 x^2 + x) \ dx = 0$ |
There is hardly a more vivid representation of the Bernoulli numbers and we award a point for that. Match score $\mathbf{13:0}$.
The Eulberian polynomials.
We admit it from the outset: the Eulberian polynomials do not exist in the literature and the name is fictitious. \begin{equation} \operatorname{\beta}_{n}(x) = \frac{1}{n+1}\, \sum_{k=0}^n (-1)^k \frac{\genfrac <> {0pt}{}{n}{k}} {\binom{n}{k}} \, x^{n-k} \quad(n \ge 0). \end{equation}Of course, $\operatorname{\beta}_{n}(1) = \operatorname{B}_{n}(1)$ as we have already seen above. What we want to emphasize here is: the Bernoulli numbers are not constants, they are the sum of n+1 terms. In other words, the coefficients of the polynomials form a regular triangle of rational numbers whose row sums are the Bernoulli numbers.
| x0 | x1 | x2 | x3 | x4 | x5 | ∑ |
|---|---|---|---|---|---|---|
| + 1 | · | · | · | · | · | 1 |
| 0 | + 1 / 2 | · | · | · | · | 1 / 2 |
| 0 | - 1/ 6 | + 1 / 3 | · | · | · | 1 / 6 |
| 0 | + 1 / 12 | - 1 / 3 | + 1 / 4 | · | · | 0 |
| 0 | - 1 / 20 | + 11 / 30 | - 11 / 20 | + 1 / 5 | · | -1 / 30 |
| 0 | + 1 / 30 | - 13 / 30 | + 11 / 10 | - 13 / 15 | + 1 / 6 | 0 |
Is it possible to find a (combinatorial) interpretation for these numbers? Perhaps building a bridge from the Bernoulli numbers to the Catalan numbers? It is worth a try.
For this purpose we introduce the following numbers generating a triangle that is the counterpart of Leibniz's harmonic triangle (which is generated when the falling factorial is used instead).
\begin{equation} \operatorname{F}(n,k) \, = \, \frac{ (n+1)^{ \overline{n} } }{ k! \, (n-k)! }. \end{equation}Then we can write
\begin{equation} \frac{\operatorname{B}_n}{\operatorname{C}_n} \, = \, \sum_{k=0}^{n} (-1)^{k} \frac{\operatorname{E}(n, k)}{\operatorname{F}(n,k)}, \end{equation}where $\operatorname{C}_n$ denote the Catalan numbers and $\operatorname{E}(n,k)$ the Eulerian numbers in their CMath form A173018.
The Akiyama-Tanigawa Algorithm.
 |
For me, this is a proof without words. Match count $\mathbf{14:0}$.
Bernoulli and Mona Lisa.
Todays long-standing mathematical conventions have many, many defects, and I can think of dozens of cases where changes would improve the current situation and make it easier on all future mathematicians.
But then we should do this! And we should do this refactoring, as it is called aptly by software engineers, with joy and without having a bad conscience.
But I would never think $\operatorname{B}_{1}$ to be anywhere near as important.
Well, it is difficult to respond to this argument. If Leonardo had decided to paint a big wart on the nose of Mona Lisa, it would also be not important. But it would hurt our aesthetic feelings. And so I perceive the Bernoulli bug: like an ugly wart on the Riemann functional equation of the zeta function.
We also have to contend with the broken windows syndrome: once shortcomings have crept in they will proliferate. Each bug confines our ability to understand the relationships. The non-natural limitation of the scope of validity of the connections between the Bernoulli numbers and other important numbers seen above is an example for this. It also means that a lot of work by mathematicians is invested to circumvent these shortcomings — effort and time that could be used for more creative thinking.
The position of some experts
For this and many other reasons over nearly 40 years of working rather heavily with Bernoulli numbers, I have been convinced by the wisdom of the convention that has long been followed by the vast majority of the major writers on mathematics.
I admit that many writers in the 20th century followed the convention $\operatorname{B}_{1}=-1/2$. Among others two very influential books adopted this choice: Nörlund's Differenzenrechnung and the Handbook of Mathematical Functions. (Match score $ \mathbf{14:2}$ ).
However, the so-called `convention´ $\operatorname{B}_{1}=-1/2$ is by no means a uniformly accepted standard, and never was. For example in Whittaker and Watson's A Course of Modern Analysis, which was a standard reference and textbook in the first half of the 20-th century, the n-th Bernoulli number is $\mid B_{2n} \mid$.
Also Jean-Pierre Serre, the first Abel Prize winner, does not adhere to the HMF convention in his book A Course in Arithmetic, which stands on the recommendation lists of many universities. Serre sets, like Whittaker and Watson, for $n \geq 1 : \ \operatorname{B}_{n}=|B_{2n}(0)| = |B_{2n}(1)|.$ So do you think Serre confuses the current generation of mathematicians? I do not think so since even a simple student of mathematics like me was able to handle his definition.
My impression is that the number of modern authors who use $\operatorname{B}_{1}=1/2$ is steadily increasing. In publications which range from the popular book by Conway and Guy, The book of numbers to the much used and valued textbook by Jürgen Neukirch, Algebraic Number Theory. Neukirch defines the Bernoulli numbers via the series expansion of $\ F(t)\, =\, B^{(1)}(t) \ $ $(\ref{B1})$ and writes (p. 427f):
The relation of the Bernoulli numbers to the zeta function gives them a special arithmetic significance. The first Bernoulli numbers are \[ B_{0}=1,\,B_{1}=\frac{1}{2},\,B_{2}=\frac{1}{6},\,B_{3}=0,\, B_{4} =-\frac{1}{30},\,B_{5}=0,\,B_{6}=\frac{1}{42}. \] In the classical literature, it is usually the function $t/(e^t-1)$, but the above definition is more natural and better suited for the further development of the theory.
In the meantime, the monograph of T. Arakawa, T. Ibukiyama, and M. Kaneko, Bernoulli numbers and zeta functions, Springer 2014, has been published, which is based on the definition $B_{1} = \frac{1}{2}$.
Generalized Bernoulli numbers.
To explain the last remark of Neukirch a little bit we look at the generalized Bernoulli numbers $B_{n,\chi}$ as defined in analytic number theory. Let $\chi$ be a Dirichlet character and $f_{\chi}$ the conductor of $\chi$. Then
\begin{equation} \sum_{n\ge 0} B_{n,\chi} \frac{t^n}{n!} := \sum_{j=1}^f \chi(j) \frac {t e^{jt}}{e^{f t}-1} . \end{equation} When $\chi = 1$, we have \begin{equation} \sum_{n\ge 0} B_{n,1} \frac{t^n}{n!} = \frac{t e^t}{e^t - 1} = \frac{t}{1-e^{-t}} \end{equation} Thus $B_{n,1} = B_n$ (which is a natural request) if and only if $B_1$ is set to $1/2$. (Match score $ \mathbf{15:2}).$
How Terence Tao introduces the Bernoulli numbers.
The way Terence Tao introduces the Bernoulli numbers in his blog The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation highlights how naturally the right choice of the recurrence leads to the generating function of the Bernoulli numbers. Therefore we cite him at length:
"We define the Bernoulli numbers $B_0, B_1, \ldots$ recursively by the formula
\begin{equation} \sum_{k=0}^{s-1} \binom{s}{k} B_k = s \label{taodef} \end{equation}
for all $ s = 1,2,\ldots $, or equivalently
\begin{equation} B_{s-1} := 1 - \frac{s-1}{2} B_{s-2} - \frac{(s-1)(s-2)}{3!} B_{s-3} - \ldots - \frac{1}{s} B_0. \end{equation}The first few values of $B_s$ can then be computed:
\[ B_0=1;\ B_1=1/2;\ B_2=1/6;\ B_3=0;\ B_4=-1/30;\ \ldots. \]From $(\ref{taodef})$ we see that
\begin{equation} \sum_{k=0}^\infty \frac{B_k}{k!} [ P^{(k)}(1) - P^{(k)}(0) ] = P'(1) \label{taopoly} \end{equation}
for any polynomial $P$ (with ${P^{(k)}}$ being the ${k}$-fold derivative of $P$); indeed, $(\ref{taodef})$ is precisely this identity with $P(x) := x^s$, and the general case then follows by linearity. "
Match score $\mathbf{16:2}$ since $(\ref{taopoly})$ is the nucleus of the Euler-Maclaurin formula and does not hold if $B_1=-1/2$. Tao then continues:
"As $(\ref{taopoly})$ holds for all polynomials, it also holds for all formal power series (if we ignore convergence issues). If we then replace $P$ by the formal power series
\begin{equation} P(x) = e^{tx} = \sum_{k=0}^\infty t^k \frac{x^k}{k!} \end{equation}we conclude the formal power series (in $t$) identity
\begin{equation} \sum_{k=0}^\infty \frac{B_k}{k!} t^k (e^t-1) = t e^t \end{equation}leading to the familiar generating function
\begin{equation} \sum_{k=0}^\infty \frac{B_k}{k!} t^k = \frac{t e^t}{e^t-1} \end{equation}for the Bernoulli numbers."
Tao's 'familiar generating function' is of course the same as our $(\ref{B1}) \ \frac{t}{{1-e^{-t}}}$.
After seeing a 21st century mathematician at work we now go back three centuries to interview two other important mathematicians: Sansei Takekazu-Kowa Seki and Jacob Bernoulli. It would be unfair not to seek their opinion. After all they invented the 'Bernoulli numbers' as they were christened by Leonhard Euler.
Sansei Takekazu-Kowa Seki's sums of equal powers.
In 1712, one year before the appearance of Bernoulli's posthumously published Ars Conjectandi, the Japanese mathematician Seki introduced the Bernoulli numbers in his work Katsuyo Sampo while developing a method to calculate sums of powers.
He called his method Ruisai Shosa-ho and explained it with reference to the following table (reproduced here shortened).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| x1 | 1 | (1) | |||||||
| x2 | 1 | 2 | (1) | ||||||
| x3 | 1 | 3 | 3 | (1) | |||||
| x4 | 1 | 4 | 6 | 4 | (1) | ||||
| x5 | 1 | 5 | 10 | 10 | 5 | (1) | |||
| x6 | 1 | 6 | 15 | 20 | 15 | 6 | (1) | ||
| x7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | (1) | |
| x8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | (1) |
| σn-1 | 1 | 1/2 | 1/6 | 0 | −1/30 | 0 | 1/42 | 0 | 1/30 |
This is obviously the binomial triangle where the bottom bar shows the Seki numbers $ \sigma_n, $ as the Bernoulli numbers could also be called for good historic reason. We learn from this computational scheme that the Seki numbers start $1,1/2, \ldots $. (Match score $\mathbf{17:2}.$ ) Seki used this table to calculate the sum of powers according to the formula:
\begin{equation} \sum_{k=1}^nk^{m-1} = \frac 1m\sum_{k=0}^{m-1}\sigma _k\binom mkn^{m-k}\qquad (n \gt 0, m \gt 0). \end{equation}And Jacob, what did you say?
... Atque si porró ad altiores gradatim potestates pergere, levique negotio sequentem adornare laterculum licet:
Summae Potestatum $\smallint n = \frac12 nn + \frac12 n \\ \smallint nn \ =\ \frac13 n^3 + \frac12 nn + \frac16 n \\ \smallint n^3 = \frac14 n^4 + \frac12 n^3 + \frac14 nn \\ \smallint n^4 = \frac15 n^5 + \frac12 n^4 + \frac13 n^3 - \frac{1}{30}n \\ \smallint n^5 = \frac16 n^6 + \frac12 n^5 + \frac{5}{12} n^4 - \frac{1}{12} nn \\ \smallint n^6 = \frac17 n^7 + \frac12 n^6 + \frac12 n^5 - \frac16 n^3 + \frac{1}{42} n \\ \smallint n^7 = \frac18 n^8 + \frac12 n^7 + \frac{7}{12} n^6 - \frac{7}{24}n^4 + \frac{1}{12} nn \\ \smallint n^8 = \frac19 n^9 + \frac12 n^8 + \frac23 n^7 - \frac{7}{15}n^5 + \frac29n^3 - \frac{1}{30} n \\ \smallint n^9 = \frac{1}{10} n^{10} + \frac{1}{2} n^9 + \frac{3}{4} n^8 - \frac{7}{10} n^6 + \frac{1}{2} n^4 - \frac{1}{12} nn \\ \smallint n^{10} = \frac{1}{11} n^{11} + \frac12 n^{10} + \frac56 n^9 - 1 n^7 + 1 n^5 - \frac12 n^3 + \frac{5}{66} n \\ $Quin imó qui legem progressionis inibi attentuis ensperexit, eundem etiam continuare poterit absque his ratiociniorum ambabimus : Sumtâ enim $c$ pro potestatis cujuslibet exponente, fit summa omnium $n^c$ seu
\[ \int n^c = \frac{1}{c + 1}n^{c+1} + \frac12 n^c + \frac{c}{2} An^{c-1} + \frac{c \cdot c - 1 \cdot c - 2}{2 \cdot 3 \cdot 4} Bn^{c-3} \]\[ +\frac{c \cdot c - 1 \cdot c - 2 \cdot c - 3 \cdot c - 4}{ 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6} C n^{c-5} \]\[ + \frac{c \cdot c - 1 \cdot c - 2 \cdot c - 3 \cdot c - 4 \cdot c - 5 \cdot c - 6 }{ 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 } Dn^{c-7} \cdots \text{& ita deinceps,} \]exponentem potestatis ipsius n continué minuendo binario, quosque perveniatur ad $n$ vel $nn$. Literae capitales A, B, C, D & c. ordine denotant coëfficientes ultimorum terminorum pro $\smallint nn,\ \smallint n^4,\ \smallint n^6,\ \smallint n^8 $ & c. nempe
\[ A = \frac16 , B = -\frac{1}{30}, C =\frac{1}{42}, D = -\frac{1}{30} \ . \] |
Summae Potestatum.
The last section above reproduces Jacob's exposition on computing sums of equal powers, as they were published in Basel in 1713, eight years after Bernoulli's death, in his book Ars Conjectandi (in the second part, on pages 97-98). We reconstruct the formula in the notation of Concrete Math, with the factorial and the falling factorial powers, as they are defined there on page 47 and 52.
\begin{align*} x^{\underline{m}} & = {\displaystyle\prod_{0\leq k\leq m-1}} \left( x-k\right) \, \quad \left( m\geq0\right) \ ; \\ x^{\underline{m}} & ={\displaystyle\prod_{m\leq k\leq-1}} \left( x-k\right)^{-1} \ \ \left( m \lt 0\right) \ . \end{align*}Bernoulli does not use the notation $\operatorname{B}_{k},$ but writes the constants either explicitly or uses the symbols A, B, C, D, …. These constants are in a one-to-one relationship with the constants $\operatorname{B}_{k}$, as can be seen from Bernoulli's formula:
\[ \operatorname{B}_{0}=1,\,\operatorname{B}_{1}=\frac{1}{2},\,\operatorname{B}_{2}=A=\frac{1}{6},\,\operatorname{B}_{3}=0,\,\operatorname{B}_{4}=B=-\frac{1}{30}, \]\[ \operatorname{B}_{5}=0,\,\operatorname{B}_{6}=C=\frac{1}{42},\,\operatorname{B}_{7}=0,\,\operatorname{B}_{8}=D=-\frac{1}{30}, \ldots \]This yields Bernoulli's Summae Potestatum in the following form:
| \begin{align} \int n^{c} & = \frac{1}{c+1}\operatorname{B}_{0}n^{c+1}+\operatorname{B}_{1}n^{c}+\frac{c}{2}\operatorname{B}_{2}n^{c-1} +\frac{c(c-1)(c-2)}{24}B_{4}n^{c-3}+ \ldots \\ & = \sum_{k\geq0}\frac{\operatorname{B}_{k}}{k!}c^{\underline{k-1}}n^{c-k+1} \end{align} |
If there is anything that deserves the name of Bernoulli numbers, these numbers are it. And although Bernoulli did not use a special notation for $\operatorname{B}_{0}$ and $\operatorname{B}_{1}$ he did use the value $\operatorname{B}_{1}=\frac{1}{2}$. (Match score $\mathbf{18:2}.$ )
And every mathematician, be it a major or a minor one who wants to change this, please stand up and explain it to the mathematical community. However, those who have changed it without giving an explanation have been guilty of counterfeiting in a particularly severe case.
Who is to blame for the confusion?
... the amount of confusion that a change would produce is vast. I find your comment that "the `confusion' would be small" the understatement of the century.
It's still a bit early in this century to decide how big this compliment really is ;-).
A look at the history of the Bernoulli numbers does not let me share this view. Earlier mathematicians such as Francois de Viete, Abraham de Moivre or Leonhard Euler referred in their papers to the Bernoulli numbers as defined by Bernoulli.

Euler's summation formula, as written by Euler.
(from D. J. Pengelley, Dances between continous and discrete.)
Thus a change was made sometimes after Bernoulli. I do not know who was the first to change it and when it happened. Nor have I heard anyone explain the reason for this change. On the other hand, the choice of $ B_n = B_n(1) $ is much more common than it seems that you assume as some outstanding mathematicians today use it in their textbooks and in their lectures, as we saw above.
So if there is a confusion, then it is already here. We have seen the example of Wikipedia's wrong definition of the Todd function and we have seen the dangers hidden in the non-natural ranges of validity of identities for Euler and Eulerian numbers if the wrong definition is chosen. So the question is only: How do we deal with the confusion?
And no, it is not `too late´ to change. Mathematicians are well prepared to handle it. To learn how to live with the risks of conventions and notations belongs to the professional training of each mathematician. This may reassure us.
What can we do?
... and what should we not do?
For instance we could introduce new names to disambiguate the two possible choices of $B_n$. In fact this has been done on the English Wikipedia and the nomenclature 'first Bernoulli numbers' and 'second Bernoulli numbers' was introduced. This disservice reflects the maximum credible misunderstanding. There is of course only one kind of Bernoulli numbers $B_{n}$.
This scholasticistic nonsense culminates on the German Wikipedia. Not only the notation $B_n^{*}$ is introduced for what is now called "Bernoulli-Zahlen zweiter Art" but the two 'kinds' are also mixed in identities like
\begin{equation} \sum_{i = m}^{n} f(i) = \sum_{j = 0}^{\infty} \frac{1}{j!} \left(B_{j}^{\ast} f^{(j-1)}(n) - B_{j} f^{(j-1)}(m)\right) . \end{equation}We can only hope that some insightful editors soon put an end to this moonshine.
Is there a canonical representation of the Bernoulli numbers?
Why is there still no canonical representation of the Bernoulli numbers? even though they are so central as Mazur writes.
… Bernoulli numbers sit in the center of a number of mathematical fields, and whenever, for a given index $k$ the Bernoulli number $\operatorname{B}_{k}$ exhibits some particular behavior, these different mathematical fields seem to feel the consequences, each in their own way. (B. Mazur, Bernoulli numbers and the unity of mathematics.)
It is this question which should really worry us because it points to a theoretical deficit, a lack of understanding.
It is my belief that this can be overcome. Consider how Euler proceeded in the similar case of the factorial numbers: He has introduced a definition, that of the gamma function, which to this day is the canonical way to interpolate the factorial numbers because it has more advantages than possible alternative definitions.
This approach characterizes progress at the highest mathematical level, which is the level of definitions. If a definition is successful it makes conventions superfluous. This objective can be achieved here as well — by introducing the Bernoulli function. Below we will give an analytic definition independent from the zeta function. This will be our substantive definition, as we called it above, in contrast to the controversial formal definitions via generating functions.
The analytical definition of the Bernoulli numbers.
Definition. The Bernoulli numbers are the values of the function $\mathcal{B}(s)$ on the non-negative integers. Here
| \begin{equation} \mathcal{B}(s) = \sum\limits_{k=0}^{\infty}\frac{\Delta^{k}\left({s}\right)}{k+1} \quad \text{ where} \quad \Delta^{k}\left({s}\right) = {\sum\limits_{v=0}^{k}}(-1)^{v}\binom{k}{v}\left(v+1\right)^{s} \ . \quad \label{berndef} \end{equation} |
In the definition ($\ref{berndef}$) we use the notation $\mathcal{B}(s)$ like we used it in the definition of the Bernoulli function $\mathcal{B}(s)=-s\zeta(1-s).$ How does that fit together?
Well, a theorem of Helmut Hasse states that this is one and the same! Hasse gives an elementary, purely real-analytic proof of this identity.
By interpreting the variable $s$ over the natural numbers, $n\leftarrow s$, and adapting the summation limit $n\leftarrow\infty$, we obtain a classic representation of the Bernoulli numbers, the Worpitzky representation (J. Worpitzky, Studien über die Bernoullischen und Eulerschen Zahlen, Crelle 94 (1883), formula (36)).
\begin{equation} \operatorname{B}_{n}=\sum_{k=0}^{n}\frac{\Delta^{k}(n)}{k+1} \ . \end{equation}
Can an embedding of discrete identities into continuous mathematics be more natural? Should we not maintain such a relationship, build on it and remove conventional obstacles from the path?
| $B_{0}$ | $1 $ |
| $B_{1}$ | $1/1 -1/2 $ |
| $B_{2}$ | $1/1 -3/2 +2/3 $ |
| $B_{3}$ | $1/1 -7/2 +12/3 -6/4 $ |
| $B_{4}$ | $1/1 -15/2 +50/3 -60/4 +24/5 $ |
| $B_{5}$ | $1/1 -31/2 +180/3 -390/4 +360/5 -120/6 $ |
| $B_{6}$ | $1/1 -63/2 +602/3 -2100/4 +3360/5 -2520/6 +720/7 $ |
Definition. Bernoulli polynomials are the values of the function $\mathcal{B}(s,x)$ at the non-negative integers $s$. Let $x$ be a real number $\gt -1$ and
\begin{equation} \mathcal{B}(s,x) = \sum\limits_{k=0}^{\infty} \frac{\Delta^{k}\left(s,x \right)}{k+1} \quad \text{where } \quad \Delta^{k}\left(s,x\right) = \sum\limits_{v=0}^{k}(-1)^{v}\binom{k}{v}\left(x+v+1\right)^{s} \ . \label{bernpolydef} \end{equation}
Hasse's theorem in its general form states
\begin{equation} \mathcal{B}(s,x) = -s \zeta(1-s,x) \ . \end{equation}
$\zeta(s,x)$ is the Hurwitz zeta function. Thus we obtain for $n \gt 0$ and real $x$
\begin{equation} \operatorname{B}_{n}(x) = -n \zeta(1-n,x) \ . \end{equation} |
The formal proof
| The infinite series $ \sum_{v=0}^{\infty}\frac{1}{n+1} \Delta_n ( {v^s} )$ converges for all complex $ s $ and represents the entire function $ - s\zeta(1-s) $, the Bernoulli function. |
We quote Hasse's proof; the translation is ours.
(I) The series $\sum_{v=0}^{\infty}\frac{1}{n+1} \Delta_n \left( \frac{1}{v^s} \right)$ converges for $\Re(s) \gt 0$ and equals there $ s\zeta(s+1)$. This results from the following formal computation:
\begin{align*} \frac{1}{v^s} &= \frac{1}{\Gamma(s)}\int_0^{\infty} e^{-vt}t^{s-1}dt, \\[6pt] \Delta_n \left(\frac{1}{v^s} \right) &= \sum_{v=0}^{n} (-1)^v \binom{n}{v}\frac{1}{(v+1)^s} \\[4pt] &= \frac{1}{\Gamma(s)}\int_0^{\infty} \sum_{v=0}^{\infty} (-1)^v \binom{n}{v} e^{-(v+1)t} t^{s-1} dt \\[4pt] &= \frac{1}{\Gamma(s)}\int_0^{\infty} \sum_{v=0}^{\infty} (1-e^{-t})^n e^{-t} t^{s-1} dt, \\[6pt] \sum_{v=0}^{\infty}\frac{1}{n+1} \Delta_n \left( \frac{1}{v^s} \right) &= \frac{1}{\Gamma(s)} \sum_{v=0}^{\infty} \int_0^{\infty} \frac{(1-e^{-t})^n}{n+1} e^{-t} t^{s-1} dt \\[4pt] &= \frac{1}{\Gamma(s)} \int_0^{\infty} \sum_{v=0}^{\infty} \frac{(1-e^{-t})^n}{n+1} e^{-t} t^{s-1} dt \qquad (*) \\[4pt] &= \frac{1}{\Gamma(s)} \int_0^{\infty} \frac{t}{1-e^{-t}}e^{-t}t^{s-1} dt \\[4pt] &= \frac{1}{\Gamma(s)} \int_0^{\infty} \sum_{n=1}^{\infty} e^{-nt} t^{s} dt \\[4pt] &= \frac{1}{\Gamma(s)} \sum_{n=1}^{\infty} \int_0^{\infty} e^{-nt} t^{s} dt \qquad \qquad \qquad \quad (**) \\[4pt] &= s \sum_{n=1}^{\infty} \frac{1}{\Gamma(s+1)} \int_0^{\infty}e^{-nt} t^{s} dt \\[4pt] &= s \sum_{n=1}^{\infty} \frac{1}{n^{s+1}} \\[4pt] &= s \zeta(s+1), \end{align*}
To justify this only the commutativity of summation and integration of $(*)$ and $(**)$ is to be shown. But this follows easily from the uniform convergence of the two sums in question
\[ \sum_{v=0}^{\infty} \frac{(1-e^{-t})^n}{n+1} e^{-t} t^{\sigma-1} dt \quad \text{and} \quad \sum_{n=1}^{\infty} e^{-nt} t^{\sigma} \qquad (\sigma=\Re(s) \gt 0) \]
which holds throughout the integration interval $ 0 \le t \le \infty $.
We use the notation $ \vec{x}_n= x_1+\ldots+x_n $ and $s^{\overline{n}} = s(s+1) \ldots (s+n-1)$.
(II) The series $\sum_{v=0}^{\infty}\frac{1}{n+1} \Delta_n \left( \frac{1}{v^s} \right)$ also converges for $\Re(s) \le 0$, uniformly in any bounded region of this half-plane. It represents the analytic continuation of $s\zeta(1+s)$ in the left half-plane.
As the starting point for the proof I choose the integral representation of the initial terms of the difference series, which is easly shown: \begin{align*} \Delta_n \left( \frac{1}{v^s} \right) & = s^{\overline{n}}\int_0^1 \ldots \int_0^1 \frac{1}{(1+\vec{x}_n)^{n+s}} dx_1 \ldots dx_n \\[4pt] & = s^{\overline{n}}\int_0^1 \ldots \int_0^1 \frac{(1+\vec{x}_n)^{-s+p}}{(1+\vec{x}_n)^{n+p}} dx_1 \ldots dx_n \end{align*} Here $p$ is an arbitrary fixed real positive number which is not an integer. For $\sigma = \Re(s) \le0$ we get the estimate \begin{align*} \left| \Delta_n \left( \frac{1}{v^s} \right)\right| & \leq \left| s^{\overline{n}} \right|(n+1)^{-\sigma+p} \int_0^1 \ldots \int_0^1 \frac{1}{(1+\vec{x}_n)^{n+p}} dx_1 \ldots dx_n \\ & = \left| \frac{s^{\overline{n}}}{p^{\overline{n}}} \right| (n+1)^{-\sigma+p} \Delta_n \left( \frac{1}{v^p} \right). \end{align*}
\begin{equation*} \text{It is well known that } \frac{1}{\Gamma(s)} \sim \frac{s^{\overline{n}}}{n! \, n^{s-1}}. \text{ Thus } s^{\overline{n}} \sim n! \, n^{s-1} \frac{1}{\Gamma(s)} \end{equation*} uniformly in any bounded region of the $s$-plane. Therefore \begin{align*} \left| \Delta_n \left( \frac{1}{v^s} \right) \right| \lesssim \frac{n! \, n^{\sigma-1} \left| \frac{1}{\Gamma(s)} \right| }{ n! \, n^{p-1} \ \frac{1}{\Gamma(p)} } n^{-\sigma+p} \, \Delta_n \left( \frac{1}{v^p} \right) = \frac{\Gamma(p)}{|\Gamma(s)|} \Delta_n \left( \frac{1}{v^p} \right) \end{align*} uniformly in any bounded region of the $s$-plane. (II) now follows from (I).
Helmut Hasse, Ein Summierungsverfahren für die Riemannsche $\zeta$-Reihe, Math. Z. 32 (1930). The paper can be freely obtained from the Center for Retrospective Digitization in Göttingen.
But no, no, ten thousand times no!
This was your response in Two Notes on Notation on the view that one should leave $0^{0}$ undefined. And it is my response to your view, that we should adopt the convention $\operatorname{B}_{1} = -1/2.$
I believe in the unity of mathematics as described by Barry Mazur and take Leonhard Euler as my advisor how to achieve such a unity: by regarding the problem as an interpolation problem which generalizes a certain sequence of rational numbers to an entire function in the complex plane.
In any case mathematics is not a bunch of disparate conventions which must be maintained in its present form just to protect some mathematicians from a possible confusion. And I would never dare to stick a number on the name of Jacob Bernoulli knowing that he himself never used it in this form.
And is there a need for a revision of Bernoulli's insights on this topic? Not at all. The embedding of the Bernoulli numbers via the Worpitzky representation into the reflected zeta function, as has been shown by Helmut Hasse, is the most convincing argument.
Let us use the function
\[ \mathcal{B}(s) = \displaystyle\sum\limits_{k=0}^{\infty}\frac{\Delta^{k}\left({s}\right)}{k+1} \]to the same beneficial effect for the Bernoulli numbers as the Euler gamma function showed for the factorial numbers. By this the Bernoulli numbers will find their natural place in mathematics, free from all conventions.
Dear Professor Knuth, thank you very much for your reply. I would like to inform you that I have posted your answer, as announced, in the newsgroup de.sci.mathematik. Since I was accused to waste your precious time with such a trivial question, I do not send you this answer directly, but leave it as my Bernoulli Manifesto on the Internet.
Sincerely,
Peter Luschny
The Bernoulli Manifesto. Copyright © 2013 by Peter Luschny. This manifesto was written on the occasion of the 300-th anniversary of the publication of Jacob Bernoulli's 'Ars Conjectandi'. Please feel free to share The Bernoulli Manifesto, which is available under the Creative Commons Attribution 3.0 Unported License. Help Jacob Bernoulli to regain the power over his numbers in the public discourse.
Join us! Sansei Takakazu-Kowa Seki, Jakob Bernoulli, von Staudt and Clausen, Worpitzky, Hasse, Neukirch, Conway and Guy, Terry Tao, …

